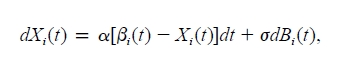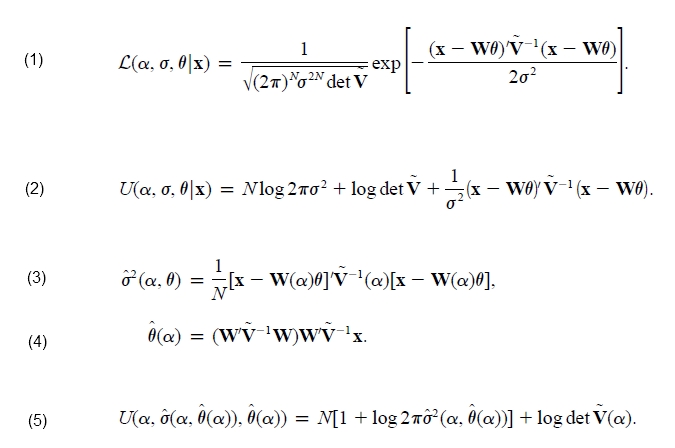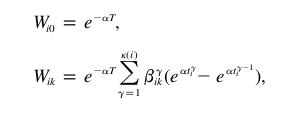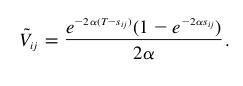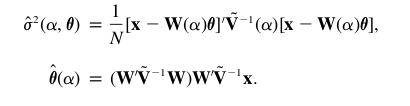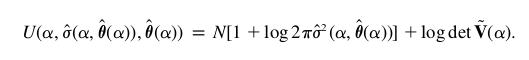Evolution of polymorphism in plants
Evolution of polymorphism in plants
Background:
- Understanding modes of species evolution is the major questions to the current evolutionary biology. As more DNA data become available, an increasing number of researchers is now switching to phylogeny-based stochastic models. Therefore, the key challenge today is to develop and test algorithms which can adequately describe evolution of phenotypes.
Goal:
- The goal of this project is to develop MCMC optimization of Ornstein-Uhlenbeck process with group-specific variance and then use it in phylogenetic comparative analysis to test for signal of directional/divergent selection in a group of plants
Mathematical tools:
- Statistics (stochastic models and MCMC) and programming. The students will learn how to use R to implement stochastic models and develop optimization procedures of the model parameters
Biological or Medical aspects:
- This kind of analysis allow to estimate the most probable way of evolution, and permit to answer a lot of question like phenotypic evolution, comparative analysis between species and more other.
Supervisors:
- Anna Kostikova & Nicolas Salamin
Students:
- Rémy Morier-Genoud
Presentation on Brownian Motion:
Implementation of Brownian Motion in Python: Code & Input examples:
Report: Project Summary & Code explanations
References:
- A Butler, A A King 2004 "Phylogenetic comparative analysis: A modeling approach for adaptive evolution" American Naturalist: 164(6): 683-695
Back to UNIL BSc course: "Solving Biological Problems that require Math 2012"
Travail séparé: estimation des paramètres les plus vraisemblables pour le modèle Ornstein-Uhlenbeck (OU)
- Le but de ce travail était d'implémenter l'algoritme donné dans l'appendice de l'article de Butler et King. Cet algoritme permet de calculer
le paramètre alpha le plus vraisemblable pour un arbre phylogénique et des traits quantitatifs donnés. Cette partie est écrite en français pour faciliter la lecture, comme la déscription du programme est peut-ètre compliquée par moments.
Etudiants:
- Georg Hoffmann
Introduction:Le modèle Ornstein-Uhlenbeck (OU)
- Pour simuler l'évolution d'un trait quantitatif, le modèle OU tient compte à la fois de la sélection, qui tend à faire évoluer le trait vers un optimum
et d'une composante aléatoire, qui représente la dérive.
pour faire une simulation avec ce modèle, il faut déterminer quelles sont les forces de sélection et de dérive, données par alpha et sigma, ainci que la valeur de l'optimum, donné ici par béta. Ces paramètres dépendent de l'arbre phylogénique et des valeurs des traits quantitatifs qu'on utilise.
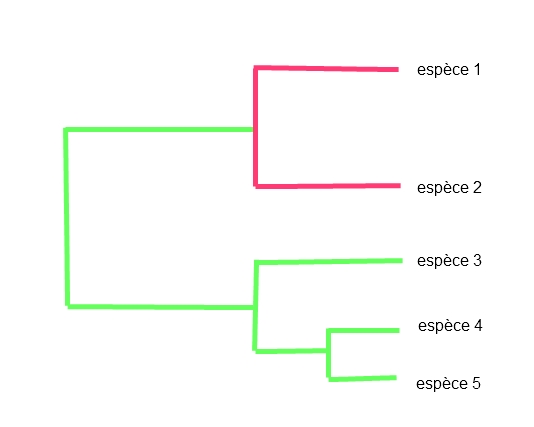
Sur cet arbre on peut voir un exemple de modèle OU avec deux optimums. les traits des espèces 1 et 2 sont soumis à un nouveau régime sélectif, caractérisé par un nouvel optimum après la spéciation des espèces 1 et 2.
Dans ce modèle, les optimums peuvent uniquement changer lors d'une spéciation et les paramètres alpha et sigma sont les mèmes pour tout l'arbre.
Le modèle pour lequel j'ai essayé d'estimer les paramètres, est la forme la plus simple du modèle OU, il n'y a qu'un optimum sélectif pour tout l'arbre.
'L'optimisation'
La vraisemblance du modèle est donnée par l'équation (1) nous utiliserons u=-2log(L) pour déterminer le maximum de L, qui est le minimum de u.
les équations (3) et (4) donnent les valeurs de sigma et theta qui annulent les dérivées partielles de u, une condition pour avoir un minimum. En utilisant ces valeurs de sigma et theta, on obtient (5), une manière d'écrire u qui ne dépend que de alpha.
c'est cette fonction u (5) qui sera minimisée pour trouver la valeur de alpha la plus vraisemblable.
L'arbre phylogénique avec dendropy:
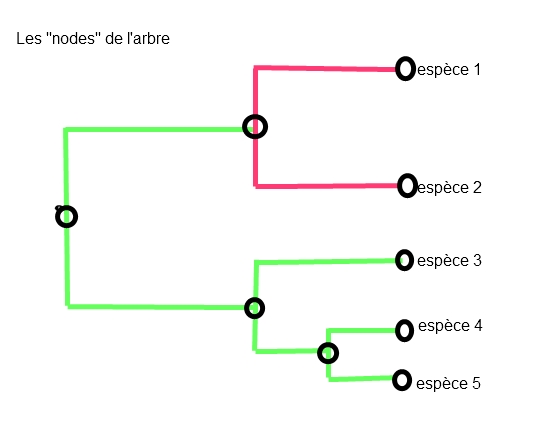
- dendropy représente l'arbre avec une série d'embranchements (nodes) qui correspondent à la racine,
aux espèces actuelles et aux embranchements internes. Chaque node a un age, un nom (label) et un node parent (sauf la raçine).
tree1 = Tree(stream=open("dated_tree2.tre"), schema="newick")
tree1.calc_node_ages(check_prec="TRUE")
ici on charge l'arbre, et on assigne les ages aux nodes.
Il y a juste un petit problème: les ages sont inversés (l'age de la raçine est le plus grand, alors qu'il doit ètre 0) Pour y remédier on détermine l'age le plus élevé, et on lui soustrait l'age du node pour trouver quel age il aurait en comptant dans le sens inverse.
first=0 for nd in tree1.age_order_node_iter(descending=True): if(first==0): T=nd.age*time first=1 rootlabel=nd.label
la Weight Matrix:
La Weight Matrix “W“ est calculée de la manière suivante:
la première colonne de la weight matrix comporte une seule valeur pour toutes les espèces: exp(-a*T), on peut donc la remplir simplement en connaissant le nombre d'espèces actuelles dans l'arbre. Ceci correspond à la colonne i0 dans la formule.
somme=0 w_prov=[] W=[] for p in range(0, nombre_especes): w_prov.append(exp(-a*T))
On peut ensuite passer à l' autre colonne de la matrice avec la seconde équation.
L'élément béta dans la formule vient d'une matrice contenant, pour chaque branche, et chaque espèce,
1 si la branche est sur le chemin évolutif de l'espèce et 0 sinon, en fait cet élément dit qu'on doit
seulement prendre les branches parentes de chaque espèce pour lesquelles on a l'optimum évolutif dont on calcule la colonne.
Pour calculer la deuxième colonne de la matrice (il y en a une par optimum sélectif +1), on a besoin d'avoir les ages des embranchements qui se trouvent sur le chemin évolutif d'une espèce, de la racine jusqu'à l'espèce actuelle. En effet, pour calculer chaque élément de la somme il faut la valeur t(y)(à gauche dans la soustraction), qui correspond à l'age du bout droit de la branche et la valeur t(y-1) qui correspond à l'age au bout gauche , pour chaque branche traversée dans l'histoire de l'espèce.
D'après la formule, On calcule la somme de l'époque 1 à l'époque actuelle, dans ce code, on fait l'inverse, ce qui ne change rien pour une somme.
On commence par prendre le node correspondant à la première espèce actuelle, puis on parcourt l'arbre en allant d'ancètre en ancètre jusqu'à la racine. À chaque fois on calcule la portion correspondante de la somme. La boucle s'arrète quand on atteint la racine de l'arbre, on a alors calculé une valeur de la colonne. On recommence pour les autres espèces actuelles.
for nd in tree1.leaf_iter(): while(nd.parent_node!=None): t2=(T-nd.age) t1=(T-nd.parent_node.age) somme=somme+exp(-a*T)*((exp(a*t2*time)-exp(a*t1*time))) nd=nd.parent_node w_prov.append(somme) somme=0
Dans le modèle simple traité ici, on peut remarquer que la somme vaut toujours :
exp(-a*T)* (exp(a*T)-exp(a*t0))
oû T est le temps actuel (final) et t0 le temps 0, à la racine. Ceci vient du fait que toutes les sommes intermédiaires s'annulent. Il faudrait un second optimum pour que certaines branches ne sient pas traversées dans le calcul, et qu'on aie une valeur différente. J'ai utilisé cette propriété pour verifier cette partie du code, les résultats étaient identiques.
W=matrix(w_prov) W.resize([2,nombre_especes]) return W.getT()
cette dernière partie était nécessaire pour éviter des erreurs avec l'optimisateur.
Le second élément qu'il faut calculer pour trouver la vraisemblance du modèle avec un alpha donné est la matrice de variance-covariance V, dont les éléments sont donnés par:
T est le temps à la fin du processus évolutif et sij est l'age du dernier ancètre commun des espèces
i et j.
Heureusement il existe une méthode dans dendropy, qui permet de trouver l'ancètre commun de deux espèces :mrca (pour most recent common ancestor). Il suffit alors de prendre l'age de ce node pour calculer sij.
def create_VM(tree1,T,a): vt=[] for nd in tree1.leaf_iter(): for nd2 in tree1.leaf_iter(): age_mrca=T-tree1.mrca(taxon_labels=[nd.label,nd2.label]).age*time vt.append((exp(-2.*a*(T-age_mrca ))*(1.-exp(-2.*a*age_mrca)) /(2.*a)) ) #vt.reverse() v=matrix(vt) v.resize([nombre_especes,nombre_especes]) return v
il faut encore noter que l'ordre “leaf_iter” est toujours le mème pour un arbre donné. Pour que les éléments soient à leur place dans les calculs, les valeurs du trait quantitatif sont mises dans le mème ordre plus loin dans le programme.
for nd in tree1.leaf_iter(): for p in range(0,len(liste_traits)): if (nd.label==liste_traits[p][0]): x2.append(float(liste_traits[p][1])) x.append(x2) x2=[]
Une fois qu'on a W et V, le reste des calculs est façile à implémenter:
sigma=(1./nombre_especes)* (matrix(x)-WM*o).getT() *VM.getI() *(matrix(x)- WM*o)
theta=(WM.getT()*VM.getI()*WM )* WM.getT()*VM.getI()*x
les méthodes getT() et getI() de numpy permettent de calculer directement les transposées et inverses des matrices W et V.
finalement on a tous les éléments pour calculer la fonction U, qui atteint son minimum quand la vraisemblance du paramètre alpha est maximale d'après les données.
U=nombre_especes*(1+log(2.*pi*sigma))+log(linalg.det(VM))
On donne alors la fonction U à un optimisateur, pour trouver la valeur de alpha qui minimise U.
fmin_l_bfgs_b(u, x0=[1], fprime=None, args=arg,approx_grad=True,bounds=mybounds)
'Résultats et conclusion'
Mon code ne donne pas les mêmes résultats que les packtages "ouch" et "geiger" disponibles pour R.
Les deux packtages donnaient aussi des valeurs différentes pour les paramètres, ce qui est déja rapporté sur quelques forums de discussion en ligne sur le sujet. Comme les codes source de ces packtages étaient difficiles à lire, je n'ai pas cherché à trouver une différence d'implémentation qui explique les résultats obtenus.
Il est probable que l'optimisateur ne trouve pas le minimum dans mon code, par manque de précision. En effet l'optimisateur trouve seulement un point oû une aproximation du gradient est presque nulle. Avec un manque de précision on peut trouver le minimum au mauvais endroit.
Je suppose que le problème est là, car un calcul à la main de W et V, avec un arbre minimal, n'avait pas montré d'erreurs et qu'une erreur est peu probable pour le calcul de sigma et theta.
En conclusion, bien que ce travail n'aie pas atteint l'objectif de déterminer correctement les paramètres qui maximisent la vraisemblance, il illustre bien les difficultés qui peuvent se présenter pour faire des simulations avec des modèles complexes et les problèmes qui peuvent survenir à cause de la précision de calcul limitée des ordinateurs.