Modeling: Pattern formation using Reaction-Diffusion models
Background: One of the most amazing properties of biological systems is their ability to form complex and organized structures. Those structures range from simple patterns (like the stripes of a zebra) to highly complex constructs (like a cell). How such structures or patterns can emerge by themselves remains a largely unsolved problem. In this project, we investigate how a simple pattern can emerge in a decentralized manner, without any plan.
Goal: The goal of the project is to understand and analyze (with computer simulations) one of the simplest and most influential pattern formation mechanism using Reaction-Diffusion models.
Mathematical tools: This project uses partial differential equations. A short introduction to partial differential equations will be provided. A mathematical software for performing simulations (matlab) will also be used.
Biological or Medical aspects: It will be investigated to which extend this model can explain the patterns observed on animals such as leopards or zebras.
Supervisor: Micha Hersch
Presentation: Media:Micha.ppt
Students: Christophe Seppey and Balazs Laurenczy
References:
The pioneering paper from Alan Turing <biblio>
- turing53chemical pmid=2185858 pdf file
</biblio> A short treatment in, Farkas, Dynamical Models in Biology, Academic Press, 2001 Media: FarkasA3.3.pdf
Contents
Mathematical background
See the Introduction to dynamical systems and differential equations Media: FarkasA3.3.pdf
(Project in Course: "Solving Biological Problems that require Math")
Développement de notre projet
I. Introduction
1.1 Notre sujet
Qui ne s'est jamais posé la question: pourquoi un zèbre est-il rayé? Une première réponse serait celle de la théorie de l'évolution en affirmant que les rayures offrent un meilleur camouflage et donc une valeur adaptative supérieure. Mais la question du "pourquoi" est fortement lié à la question du "comment": comment un zèbre obtient-il ses rayures? Pour répondre à cette question, il faut s'intéresser de plus près à l'aspect moléculaire de la formation des rayures.
Le modèle d'Allan Turing (article écrit en 1952) affirme que l'interaction entre certaines molécules amène la " surface " du zèbre à se différencier en fonction des concentrations de chacune des dites molécules. Dans ce modèle, on trouve un activateur et un inhibiteur où la présence de l'activateur induira la production de l'inhibiteur tandis que la présence de l'inhibiteur induira la destruction de l'activateur. En résumé, plus il y a d'activateur, plus il y a d'inhibiteur, mais plus il y a d'inhibiteur, moins il y a d'activateur donc moins il y a d'inhibiteur et donc plus il y a d'activateur... et ainsi de suite jusqu'à ce qu'il y ait stabilisation des concentrations moléculaire et donc, si on est pas trop malchanceux, formation d'un motif.
Afin de comprendre ce processus, il nous faudra utiliser les équations différentielles qui nous permettent de mettre en interaction plusieurs paramètres simultanément (concentrations, position, temps). Pour ce faire, on utilisera un logiciel de traitement de matrice: Matlab.
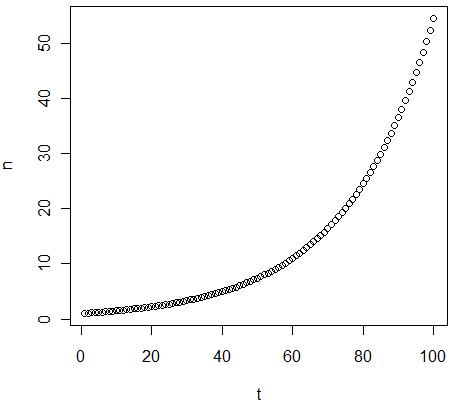
1.2 Principes de base des équations différentielles : petite histoire d'une population (semaine 3)
Pour comprendre les équations différentielles, prenons un exemple intuitif, la dynamique d'une population. Le taux de variation du nombre d'individus d'une population est soumis à deux facteurs: le taux de natalité et le taux de mortalité et c'est la somme de ces deux taux qui donnera la variation du nombre d'individus à chaque génération. Si ce taux est positif, la taille de la population augmentera à l'infini et s'il est négatif, la taille de la population diminuera jusqu'à disparition.
Mais évidemment, le taux de natalité et de mortalité dépendent de la taille de la population. En effet, plus il y a d'individus, plus il y a de nouveaux-nés et de décès. Considérant ceci, nous pouvons aisément comprendre que si le taux de variation est positif, plus la population sera grande, plus sa taille augmentera rapidement et au contraire si le taux de variation est négatif : plus la population sera grande plus sa taille diminuera vite.
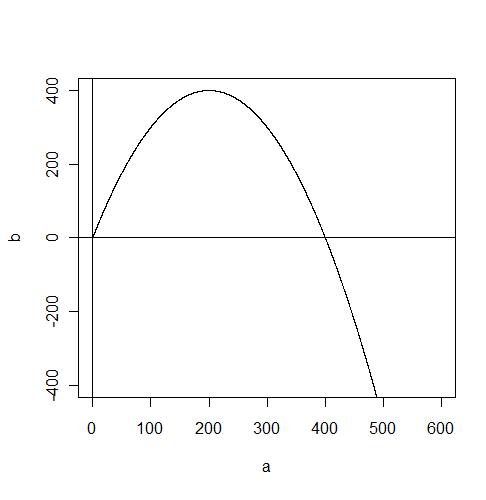
Nous pouvons aussi remarquer qu'il existe des points où la taille de la population reste stable. Ces points sont appelé points fixes. Parmi ces points fixes, il y a la solution triviale où le taux de variation est nulle et donc la taille de la population ne change pas. Mais il existe des points fixes plus intéressant où malgré un taux de variation non nulle, la taille de la population reste stable. Ces points stables sont les endroits où, étant une taille de population donnée, le taux de natalité compense exactement le taux de mortalité. Ce point fixe peut avoir deux états : instable ou stable. En effet, avec un taux de variation positif, aussitôt que la taille de la population s'écarte légèrement de ce point, on assistera à une augmentation de la population et on ne retournera pas au point fixe. Nous qualifions donc ce point d'instable. Au contraire, avec un taux de variation positif, la population pourra avoir n'importe quel taille, elle tendra toujours à diminuer et à atteindre le point fixe et, une fois atteint, à ne plus bouger (stable).
Ce modèle simple peut aussi s'appliquer à d'autres type de courbe (parabolique, logarithmique, etc), le nombre et l'état des points fixes étant déterminés par la manière dont la courbe coupe l'axe des x. Si la courbe a une pente positive, elle a un taux de variation positive et c'est donc un point instable. A l'inverse, une pente négative engendre un point stable.
Dans notre projet, on s'intéressera à un modèle de diffusion-réaction où ce ne sera plus la taille d'une population qui variera en fonction d'elle même mais la concentration de deux molécules en fonction de leur position sur une surface et des concentrations respectives des dites molécules.
II. Dans le vif du sujet
2.1 Première étape : systèmes de diffusion à 1 dimension sur Matlab (semaine 6)
Après avoir appris la base de la base de Matlab, nous nous sommes attaqué à résoudre des équations différentielles.
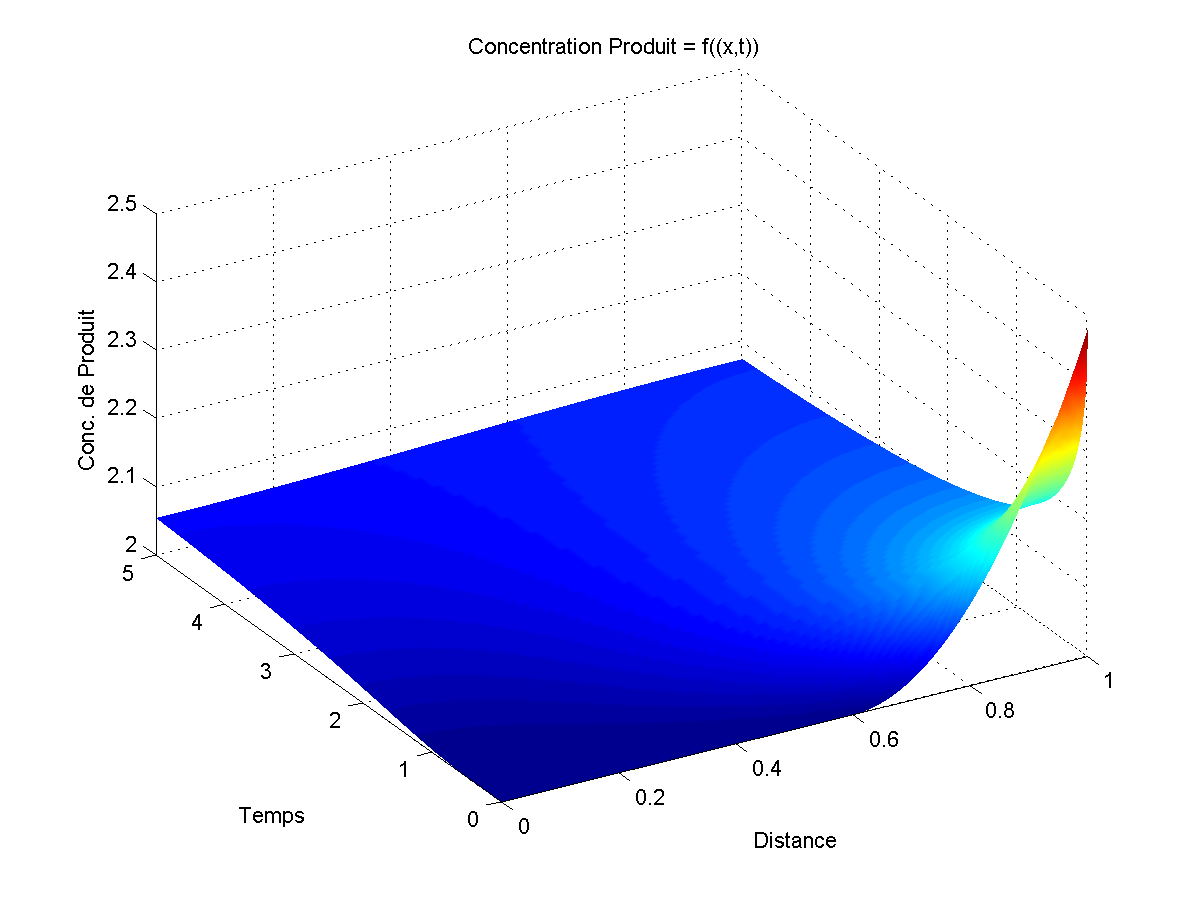
La seconde étape consista à produire des graphiques de diffusion à une dimension. On peut résumer le système à un cylindre de longueur x et de diamètre négligeable, rempli d'un fluide avec différentes concentrations moléculaire selon l'endroit du cylindre. Si on laisse les molécules diffuser, elles se déplaceront des endroits les plus concentrés aux endroits les moins concentrés et cela, d'autant plus vite que la concentration au lieux de départ est grande. Une fois la diffusion terminée, toutes les concentrations en fonction de x seront égales ce qui peut être assimilé à un point fixe stable.
Les graphiques étaient composés de trois axes: x = la position dans le tube, t = le temps et u = la concentration en fonction de la position dans le tube et du temps.
On peut résumer le problème avec la fonction suivante:
∂c/∂t = D • ∂2c/∂x2
où
- ∂c/∂t est la dérivée de la concentration en fonction d'un temps t, c'est à dire le changement de concentration à un temps donné.
- D est le coefficient de diffusion (plus D est grand, plus vite se nivelleront les concentrations dans le tube).
- ∂2c/∂x2 est la dérivée seconde de la concentration en fonction de la position dans le tube.
Sur Matlab, le traitement de l'équation se faisait par l'utilisation de la fonction pdepe.
Pour résumer rapidement, la fonction pdepe renvoie une matrice de la concentration en fonction de la position (différentes colonnes) et du temps (différentes lignes). En plus du nombre de positions (x) et du nombre d'écart de temps (t) qui donnent les dimentions de notre matrice, on doit aussi définir d'autres facteurs (voir " help pdepe ").
Le premier facteur à définir est la fonction définissant les conditions initiales des concentration en fonction de la position (icfun). Pour les paramètres, on peut mettre à peu près n'importe quoi tant que c'est une fonction allant d'un bout à l'autre des positions de x.
Le second facteur (pdefun) renverra les paramètres d'une fonction (formule 2-2 dans "help pdepe "). En résumé, il faut mettre des paramètres c, f et s qui transforme ce monstre en la fonction de diffusion donné quelques lignes plus haut.
Les autres facteurs (m et bcfun) sont quant à eux un peu plus nébuleux. m renvoi au facteur m dans la formule 2-2 donc dans notre cas, m = 0. Quant à bcfun, on sait seulement que ces paramètres donnes les conditions au bord du graphique.
Une fois tout cela compris, il ne reste plus qu'à faire un graphique de la concentration (z) en fonction du temps (x) et de la position (y) à partir de la matrice donnée par la fonction pdepe.
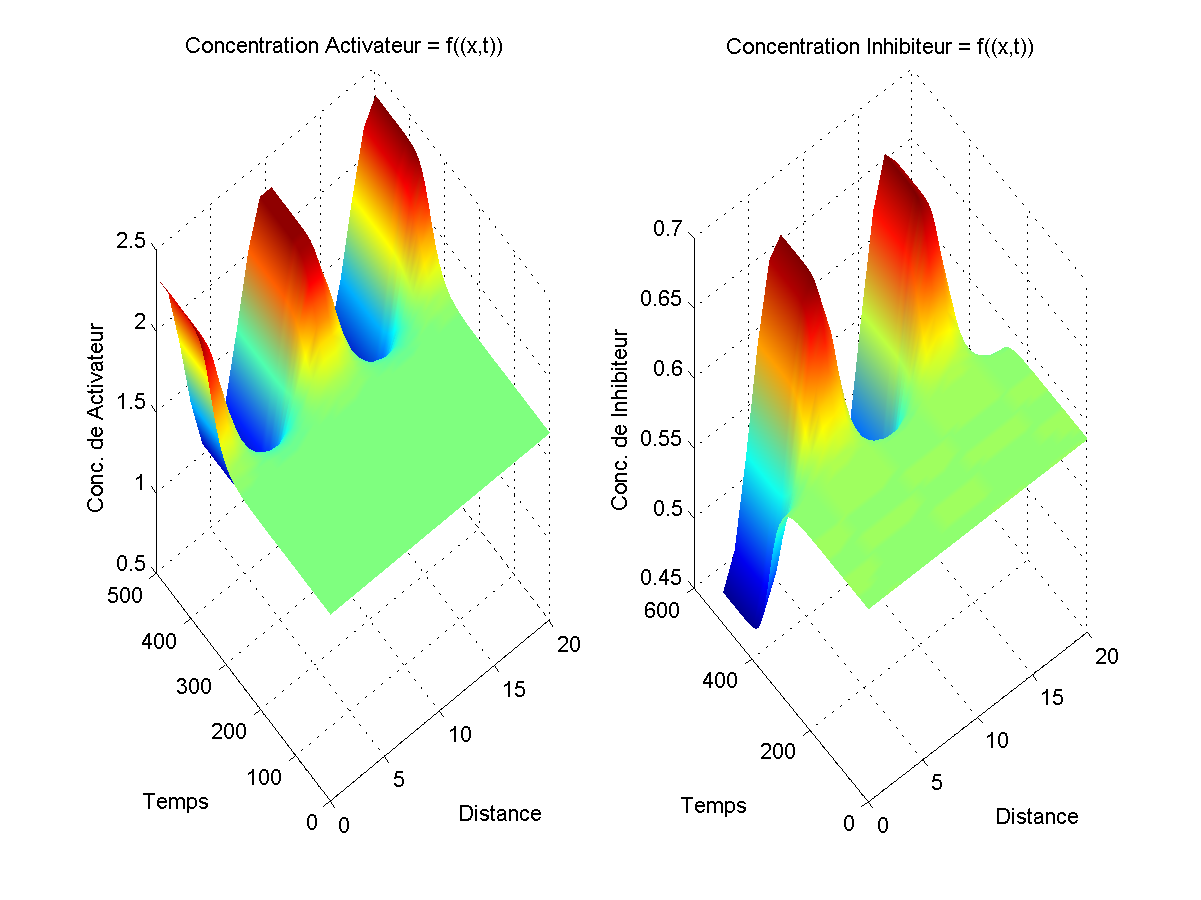
2.2 Système de diffusion/réaction à 1 dimension (semaine 6)
Comme le but du projet est de se servir d'un un modèle de diffusion/réaction afin de faire apparaître des motifs sur une surface (2 dimensions), nous avons dû passer par l'étape de la diffusion/réaction à 1 dimension.
À cette étape ci, la question devient beaucoup plus biologique. En effet, avant, nous avions seulement la diffusion passive d'une molécule, ce qui faisait assez chimique, tandis qu'avec le modèle de diffusion/réaction développé par Allan Turing, on a, comme dit dans l'introduction, deux molécules qui interagissent entre elles: un activateur et un inhibiteur. La présence de l'activateur induira la production de l'inhibiteur tandis que la présence de l'inhibiteur induira la destruction de l'activateur (plus il y a d'activateur, plus il y a d'inhibiteur, moins il y a d'activateur, moins il y a d'inhibiteur, plus il y a d'activateur...).
Nous avons réussi à tester deux modèles qui donnent des résultats concluants. Ici, les modèles auront bien sûr des variations dans les concentrations d'activateur et d'inhibiteur.
2.2.1 Premier modèle
Dans les formules donnant la variation de concentration d'activateur et d'inhibiteur en fonction du temps, il faudra prendre en compte:
- la dérivée seconde des concentrations en fonction de la position multipliée pas le coefficient de diffusion ∂2c1/∂x2 * D1 et ∂2c2/∂x2 * D2 ; - les concentrations d'activateur (f(c1,c2)) et d'inhibiteur (g(c1,c2)) déjà présente selon les formules suivantes:
∂c1/∂t = ∂2c1/∂x2 * D1 + f(c1,c2)
∂c2/∂t = ∂2c2/∂x2 * D2 + g(c1,c2)
avec des fonctions qui expriment la concentration d'activateur et d'inhibiteur en fonction de leurs concentrations respectives:
f(c1,c2) = a1 * c1 * c2 – k1 * c1 + s1
g(c1,c2) = a2 * c1 * c2 - k2 * c2 + s2
En plus de ces formules, on nous a précisé trois autres conditions de Turing à respecter:
f(c1,c2) = g(c1,c2) = 0;
∂f/∂u1 < 0;
∂g/∂u2 > 0;
D1 < D2 (coefficient de diffusion de l'activateur inférieur à celui de l'inhibiteur)
Avec ces renseignements, il ne nous restait plus qu'à trouver des valeurs de a1, a2, k1, k2, s1, s2 qui respectaient ces règles.
Encore ici, il s'agit de trouver les bons coefficients de c, f et s à mettre dans la formule 2-2 exprimée dans l'aide de pdepe de Matlab mais ici, on doit définir deux fois chaque coefficient c, f et s; une fois pour l'activateur et une fois pour l'inhibiteur.
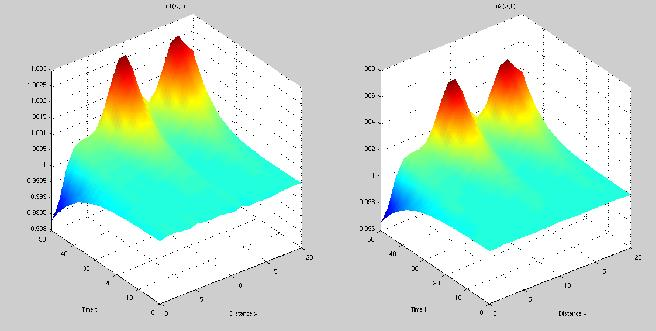
Graphiquement, ce modèle a l'avantage de toujours donner des motifs (concentration d'activateur et d'inhibiteur différentiel selon la position) mais a le désavantage de voir, une fois ces motifs "en place", les concentrations d'activateur et d'inhibiteur continuer à augmenter.
2.2.2 Deuxième modèle
Dans ce deuxième modèle, seul les formules donnant les concentrations en fonction des concentrations respectives (f(c1,c2), g(c1,c2)) sont changées. Elles deviennent:
f(c1,c2) = a1 - c1 + c2 * c12 g(c1,c2) = a2 – c2 * c12
Avec ce modèle, l'avantage est que, quand il fonctionne, non seulement les motifs sont présents, mais ils restent stables (les concentrations ne bougent plus en fonction du temps). Le problème est qu'il faut faire une vingtaine d'essais avent de tomber sur un motif, les autres fois, le motif de départ a plus d'amplitude que le motif final. Exemple simple: comme un zèbre qui aurait plus de rayures au début de son développement qu'une fois adulte?!? On doit aussi dire qu'on ne peut pas travailler avec n'importe quels coefficients.
Si on regarde les deux graphiques, on dirait qu'au temps 0, on a une ligne droite ce qui est presque le cas. En effet, si la ligne était parfaitement droite, il n'y aurait pas de réaction et c'est pour ça que l'on ajouter un facteur aléatoire (négligeable par rapport aux valeurs de concentration finales) ce qui permet de produire un motif. Ces deux modèles, partant de conditions simples et se complexifiant avec le temps sont un bon exemple de point fixe instable; le petit facteur aléatoire suffisant à faire "partir" le système.
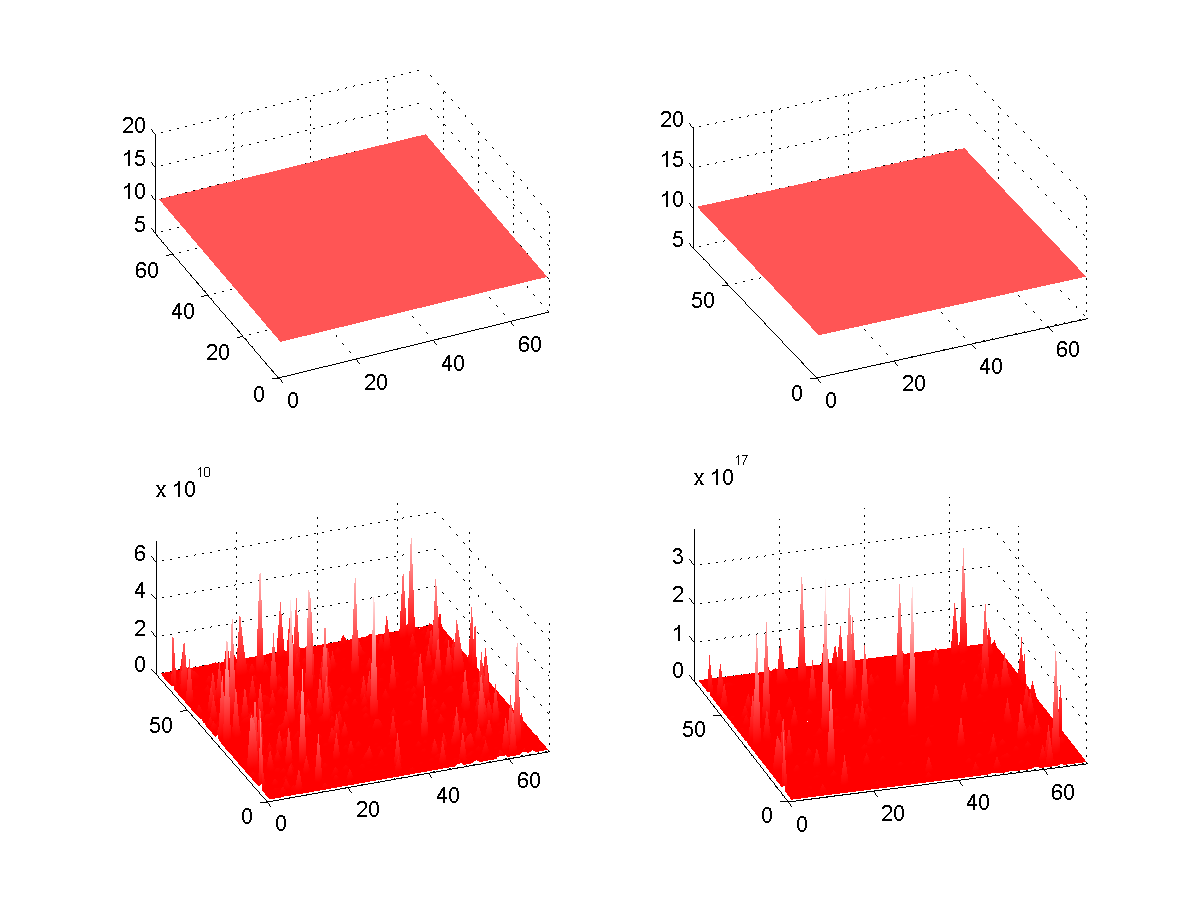
2.3.1 Système diffusion/réaction à 2 dimensions dans l'espace: l'oeuvre inachevée! (semaine 11)
Après avoir compris les diffusions et diffusion/réaction à 1 dimension, l'étape suivante était de faire un modèle de diffusion/réaction à 2 dimensions. Ici, on a dû prendre la fonction parabolic de Matlab, la fonction pdepe n'étant plus assez complète pour pouvoir faire la diffusion à 2 dimensions.
Avec cette nouvelle fonction, on devait d'abord définir une surface avec la fonction pdetool. Les paramètres de cette fonction tiennent compte d'une surface (définie par des points en x,y (p), des coordonnées des triangles formés pas les points (t) et de données relatives au côtés des triangles (e)), des conditions au bord (b) et de la formule duquel seront extrait les concentration des activateur et inhibiteur. Cette fonction est la même que dans le système de diffusion simple et on doit encore donner les coefficients qui conviennent sur une fonction comprise par la fonction parabolic de façon à obtenir la fonction du début.
fonction à obtenir:
∂c1/∂t = ∂2c1/∂x2 * D1 + f(c1,c2)
∂c2/∂t = ∂2c2/∂x2 * D2 + g(c1,c2)
...avec la fonction:
d * (∂c/∂t) – c * ∂2c/∂x2 + a * c = f
ou autrement:
d * (∂c/∂t) = c * ∂2c/∂x2 + a * c + f
Pour avoir les bon coefficient, on met d = 1, c = taux de diffusion, a = 0, et f = la fonction de notre activateur ou inhibiteur. On doit aussi définir les conditions initiales de concentration (u_old, v_old; respectivement de l'activateur et de l'inhibiteur) et l'intervalle de temps (tlist).
Tout d'abord on devait faire une surface à partir de la fonction pdetool. Cette fonction nous envoie vers un interface où on peut dessiner une forme. Cette forme sera définie par les conditions de Neuman pour les bordure et parabolique pour la PDE, on exporte les conditions de bordure et le mesh dans matlab où on pourra les utiliser dans notre formule.
Malgré tout nos effort, les résultats n'ont pas été très concluant. Les concentrations finissaient toujours par se diffuser de manière homogène ce qui ne révélait aucun motif. Les causes de cet "échec" sont soit une mauvaise compréhension de la fonction où soit le fait que les coefficients pour obtenir le pattern sont difficiles à cerner.
'2.3.2 La matrice notre sauveuse: rebondissement finale (semaine 14)'
Après les résultats peu concluant avec la fonction parabolic, nous étions un peu dépités et commencions à nous faire à l'idée de devoir remettre un travail dont le but n'aurait pas été atteint. Lors de la dernière séance avec l'assistant, voyant que la fonction parabolic ne fonctionnait pas comme prévu, nous avons eu l'idée de faire interagir les molécules sur deux matrices carrées (activateur et inhibiteur) où la surface serait donnée en fonction des colonnes et rangées et où la valeur de chaque cellules donnerait la concentration de chaque molécules. C'était une idée exploitable mais le temps faisait défaut et il nous fallait penser à la présentation.
Malgré tout, Balazs décida quand même d'essayer de faire le code. Le résultat est que les concentrations varient sur la surface mais qu'on ne peut pas dire si les points restent au même endroit en fonction du temps. On voit par contre que le motif est au départ presque uniforme et qu'à la fin, il y a de grande différences de concentration en fonction de l'espace ce qui est un bon exemple de point fixe instable.
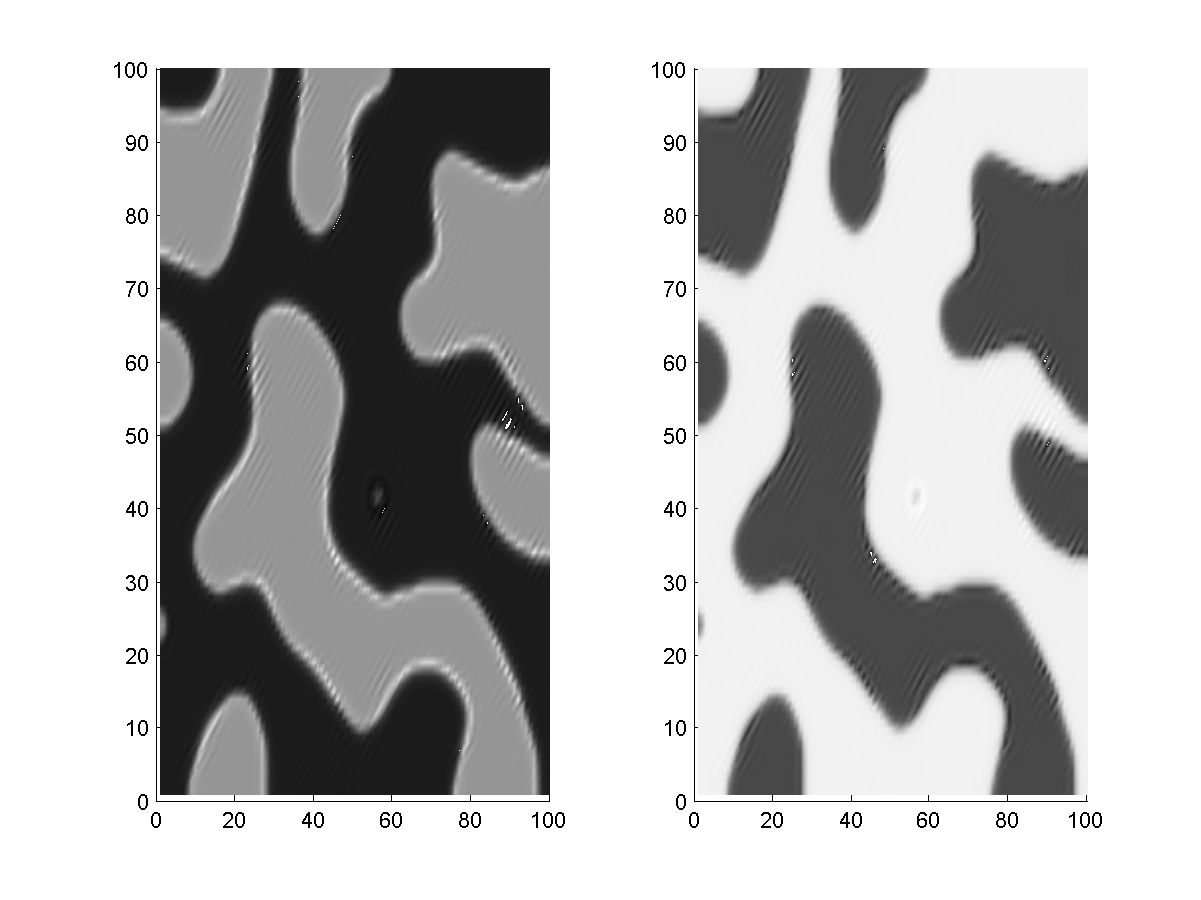
2.3.3 Un petit miracle avant la fin (jour J - 17H)
Encore ici, Balazs l'infatigable, décida de pousser l'affinement du modèle matriciel jusqu'au dernier moment... et il a bien fait. Après avoir travaillé sur les coefficients et vérifié une dernière fois les conditions, il réussit à obtenir un motif presque parfait. Pas de concentrations négatives, des concentration n'extrapolant pas vers l'infini et un motif stable dans l'espace.
III. Conclusion
Au final, nous avons, quoique in extremis, atteint tous nos objectifs. Ce travail nous a aussi permis une meilleur compréhension des équations différentielles et une certaine aptitude à travailler avec Matlab. Une meilleur connaissance du programme et de ses fonctions nous aurait sûrement permis d'aller plus loin dans le projet et peut-être d'obtenir des motifs d'autre manière comme avec la fonction parabolic ou encore en essayant d'autres coefficients, d'autres formules ou un modèle avec plus de molécules interagissant entre elles. Nous aurions aussi pu changer de programme par exemple R ou Lstudio. En résumé, les pistes à explorer n'auraient pas manqué et il aurait été intéressant de voir où nous aurions pu aller avec plus de temps.
[projet par Christophe Seppey et Balazs Laurenczy, écrit par Christophe Seppey]