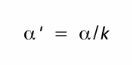Difference between revisions of "Pathway enrichment in DNAse1 footprinting data"
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
'''Background''': Il est essentiel pour le domaine de la génétique d’éclaircir le réseau de transcription qui est impliqué dans les cellules humaines. Actuellement, des données couvrant une grande partie du génome sont accessibles au public et permettent alors une réelle avancée dans la compréhension de la régulation de la transcription. | '''Background''': Il est essentiel pour le domaine de la génétique d’éclaircir le réseau de transcription qui est impliqué dans les cellules humaines. Actuellement, des données couvrant une grande partie du génome sont accessibles au public et permettent alors une réelle avancée dans la compréhension de la régulation de la transcription. | ||
| − | ''' | + | '''But''': Le but du projet était d’identifier des motifs spécifiques qui se retrouvent dans certaines voies biologiques (pathways) en cartographiant des réseaux des facteurs de transcriptions (TF). Nous souhaitions donc savoir quels TF sont impliqués dans quelles voies. Ces résultats pourraient ensuite servir d'outils pour, par exemple, identifier des dysfonctionnements dans une voie particulière ou augmenter les connaissances concernant les interactions TF-pathways. |
| − | ''' | + | '''Outils mathématiques''': Pour la création et la gestion de nos bases de données, nous avons utilisé le programme SQLite, qui permet la mise en lien très efficace de nombreuses tables entre elles. |
Pour la mise en place de requêtes et tests statistiques, nous avons opté pour le programme libre R. | Pour la mise en place de requêtes et tests statistiques, nous avons opté pour le programme libre R. | ||
Le test statistique est basé sur une distribution hypergéométrique (loi des tirages sans remise). Nous avons par ailleurs essayé de corriger pour les tests multiples (Bonferroni). | Le test statistique est basé sur une distribution hypergéométrique (loi des tirages sans remise). Nous avons par ailleurs essayé de corriger pour les tests multiples (Bonferroni). | ||
| − | + | ||
| + | [[Image:Gig 1.png]] | ||
| + | |||
Fig.1 : Calcul de la p-value avec distribution hypergéométrique. | Fig.1 : Calcul de la p-value avec distribution hypergéométrique. | ||
| + | |||
| + | |||
| + | [[Image:fig 2.png]] | ||
| + | |||
| + | Fig.2 :Permet d’ajuster la p-value lors de test multiple. Le seuil de rejet α <5% pour compenser le nombre de tests (k). | ||
| + | |||
| + | |||
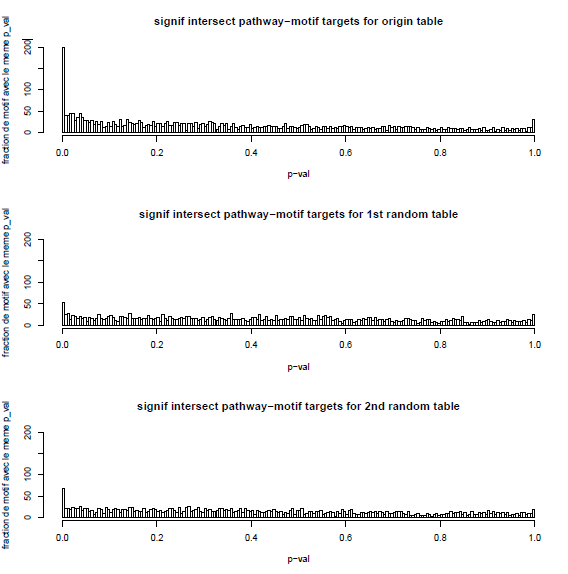
| + | '''Résultats''':Nous nous sommes intéressés au recouvrement entre les motifs des gènes de la lignée 'HSMM' (muscle squelettique humain) et les voies biologiques de cette même lignée cellulaire. Les recouvrements ayant une p-value significative montrent qu'il y a enrichissement. | ||
| + | |||
| + | [[Image:fig 3.png]] | ||
| + | |||
| + | Fig.3 : Histogrammes de nos p-values, avec permutation aléatoires des motifs pour les histogrammes 2 et 3. | ||
| + | |||
| + | |||
| + | On remarque un signal proche de p-val=0 qui semble intéressant et laisse penser qu’il y a eu un enrichissement. Une série de permutation de la table de données permet de vérifier que le signal observé n’est pas dû au hasard. | ||
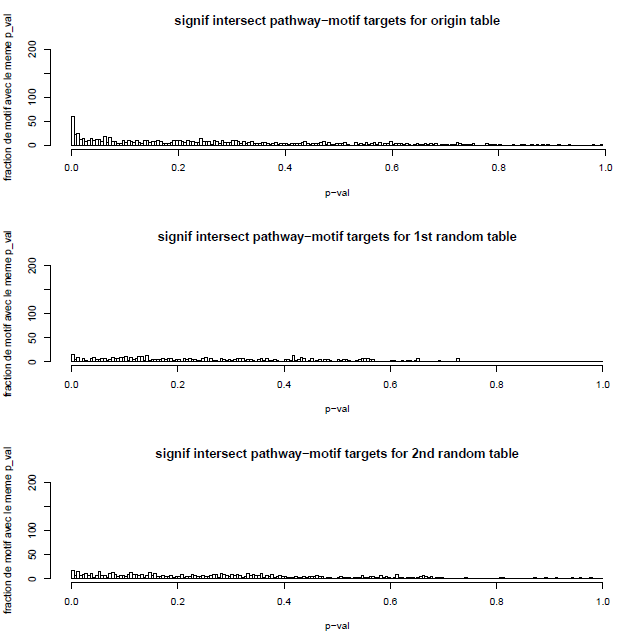
| + | Nos résultats les plus significatifs sont impliqués dans des pathways très générales, comme le système immunitaire, qui se retrouvent dans de nombreuses lignées et impliquent de nombreux gènes, donc fortement susceptibles d’avoir d’autres fonctions. Afin d'être plus spécifiques à 'HSMM', nous avons restreint notre analyse aux voies impliquant moins de 50 gènes. Le résultat est identique au précédent, malgré un signal plus faible dû à un plus petit nombre de résultats. | ||
| + | |||
| + | [[Image:fig 4.png]] | ||
| + | |||
| + | Fig.4 : Histogrammes de nos p-values en limitant à 50 gènes par pathway, avec permutation aléatoire des motifs pour les histogrammes 2 et 3. | ||
| + | |||
| + | |||
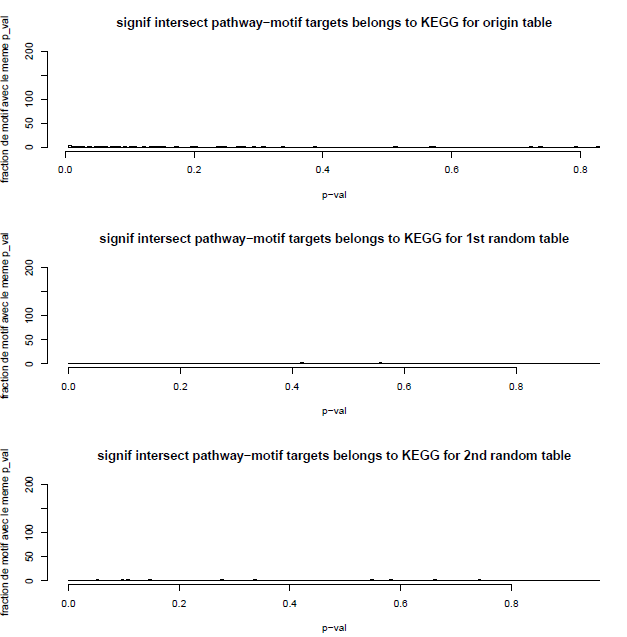
| + | Finalement, nous avons encore limité notre recherche aux pathways issues uniquement de la librairie KEGG afin de pouvoir reconstruire, de manière qualitative, un schéma d'interactions comparable à d'autres données déjà publiées. | ||
| + | |||
| + | [[Image:fig 5.png]] | ||
| + | |||
| + | Fig.5 : Histogrammes de nos p-values limités au pathway issues de KEGG, avec permutation aléatoire des motifs pour les histogrammes 2 et 3. | ||
| − | |||
| − | |||
| − | ''' | + | [[Image:fig 6.png]] |
| + | |||
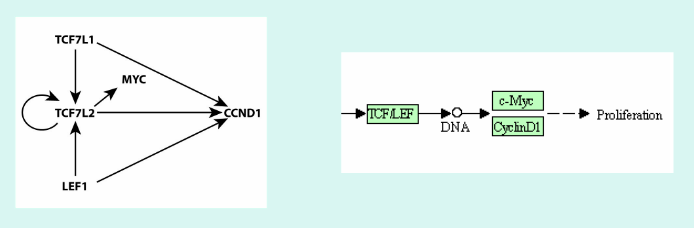
| + | Fig.6 : Schéma représentant les interactions entre les gènes (top 5 de nos p-values résultant de la table 1 de la figure 5) impliqués dans la pathway du cancer de la thyroïde. A gauche, celui que nous obtenons versus, à droite, celui issu de KEGG. | ||
| + | |||
| + | |||
| + | Les schémas sont quasiment identiques, ce qui implique que nos résultats semblent corrects. Il faudrait encore vérifier si les séquences des motifs des gènes LEF1 et TCF7L sont identiques et similaires, afin de diminuer le nombre de flèches impliquées et donc la densité du réseau. | ||
| + | Contrairement au modèle de distribution utilisé (loi hypergéométrique), nos résultats ne sont pas indépendants, c’est-à-dire qu’on a possiblement des données chevauchantes. Une même paire motif-footprint peut être semblable pour 2 gènes ou plus, à plus forte raison lorsque l'on se focalise sur une voie biologique donnée, puisque les gènes relatifs sont très souvent physiquement proches ('cluster'). La comptabilisation augmente le nombre de résultats et mène à une surévaluation des p-values. Nos résultats sont donc biaisés. | ||
| + | |||
| + | [[Image:fig 7.png]] | ||
| + | |||
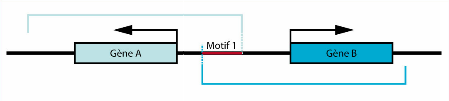
| + | Fig.7 : Schéma représentant le chevauchement. Deux gènes étant régulés par le même motif. | ||
| + | |||
| + | |||
| + | |||
| + | '''Conclusion''':Nous obtenons un résultat intermédiaire sensé et prometteur. Mais nos valeurs de p étant biaisées, notre analyse mérite d'être réitérée de manière plus rigoureuse. | ||
| + | |||
| + | '''Perspectives''':Pour la suite, il est nécessaire de prendre en compte cet effet de chevauchement pour ne compter qu’une fois les motifs et ainsi pourvoir appliquer une correction de Bonferroni, l’analyse correspondant cette fois au modèle de la distribution hypergéométrique. Il est donc important de nettoyer de manière plus rigoureuse les données avant l’analyse. | ||
| − | ''' | + | '''Superviseurs''': [[User:Aurelien | Aurelien Mace]] & [[User:David|David Lamparter]] |
| − | ''' | + | '''Étudiantes''':Sabine Mentha, Emmanuelle Besson et Dehlia Chevalley |
| − | ''' | + | '''Présentation''':PREZI [[http://prezi.com/r5vkvgut9rje/pathway-enrichment-dnase1-footprinting-data/?auth_key=9b813e906225faf8b46b75e1e22aa0aee1dc3109&kw=view-r5vkvgut9rje&rc=ref-41624103]] |
| − | ''' | + | '''Références''': |
| + | Librairie KEGG, http://www.genome.jp/kegg/ , [site web], consulté le 30.05.2013 | ||
| + | Circuitry and Dynamics of Human Transcription Factor Regulatory Networks, Shane Neph et al., cell 150,p.1274-1286, 14 septembre 2012 | ||
| + | An expansive human regulatory lexicon encoded in transcription factor footprints, Neph et al,Nature,2012 | ||
| − | Back to [[UNIL BSc course: "Solving Biological Problems that require Math | + | Back to [[UNIL BSc course: "Solving Biological Problems that require Math 2013"]] |
Latest revision as of 17:46, 6 June 2013
Background: Il est essentiel pour le domaine de la génétique d’éclaircir le réseau de transcription qui est impliqué dans les cellules humaines. Actuellement, des données couvrant une grande partie du génome sont accessibles au public et permettent alors une réelle avancée dans la compréhension de la régulation de la transcription.
But: Le but du projet était d’identifier des motifs spécifiques qui se retrouvent dans certaines voies biologiques (pathways) en cartographiant des réseaux des facteurs de transcriptions (TF). Nous souhaitions donc savoir quels TF sont impliqués dans quelles voies. Ces résultats pourraient ensuite servir d'outils pour, par exemple, identifier des dysfonctionnements dans une voie particulière ou augmenter les connaissances concernant les interactions TF-pathways.
Outils mathématiques: Pour la création et la gestion de nos bases de données, nous avons utilisé le programme SQLite, qui permet la mise en lien très efficace de nombreuses tables entre elles. Pour la mise en place de requêtes et tests statistiques, nous avons opté pour le programme libre R. Le test statistique est basé sur une distribution hypergéométrique (loi des tirages sans remise). Nous avons par ailleurs essayé de corriger pour les tests multiples (Bonferroni).
Fig.1 : Calcul de la p-value avec distribution hypergéométrique.
Fig.2 :Permet d’ajuster la p-value lors de test multiple. Le seuil de rejet α <5% pour compenser le nombre de tests (k).
Résultats:Nous nous sommes intéressés au recouvrement entre les motifs des gènes de la lignée 'HSMM' (muscle squelettique humain) et les voies biologiques de cette même lignée cellulaire. Les recouvrements ayant une p-value significative montrent qu'il y a enrichissement.
Fig.3 : Histogrammes de nos p-values, avec permutation aléatoires des motifs pour les histogrammes 2 et 3.
On remarque un signal proche de p-val=0 qui semble intéressant et laisse penser qu’il y a eu un enrichissement. Une série de permutation de la table de données permet de vérifier que le signal observé n’est pas dû au hasard.
Nos résultats les plus significatifs sont impliqués dans des pathways très générales, comme le système immunitaire, qui se retrouvent dans de nombreuses lignées et impliquent de nombreux gènes, donc fortement susceptibles d’avoir d’autres fonctions. Afin d'être plus spécifiques à 'HSMM', nous avons restreint notre analyse aux voies impliquant moins de 50 gènes. Le résultat est identique au précédent, malgré un signal plus faible dû à un plus petit nombre de résultats.
Fig.4 : Histogrammes de nos p-values en limitant à 50 gènes par pathway, avec permutation aléatoire des motifs pour les histogrammes 2 et 3.
Finalement, nous avons encore limité notre recherche aux pathways issues uniquement de la librairie KEGG afin de pouvoir reconstruire, de manière qualitative, un schéma d'interactions comparable à d'autres données déjà publiées.
Fig.5 : Histogrammes de nos p-values limités au pathway issues de KEGG, avec permutation aléatoire des motifs pour les histogrammes 2 et 3.
Fig.6 : Schéma représentant les interactions entre les gènes (top 5 de nos p-values résultant de la table 1 de la figure 5) impliqués dans la pathway du cancer de la thyroïde. A gauche, celui que nous obtenons versus, à droite, celui issu de KEGG.
Les schémas sont quasiment identiques, ce qui implique que nos résultats semblent corrects. Il faudrait encore vérifier si les séquences des motifs des gènes LEF1 et TCF7L sont identiques et similaires, afin de diminuer le nombre de flèches impliquées et donc la densité du réseau.
Contrairement au modèle de distribution utilisé (loi hypergéométrique), nos résultats ne sont pas indépendants, c’est-à-dire qu’on a possiblement des données chevauchantes. Une même paire motif-footprint peut être semblable pour 2 gènes ou plus, à plus forte raison lorsque l'on se focalise sur une voie biologique donnée, puisque les gènes relatifs sont très souvent physiquement proches ('cluster'). La comptabilisation augmente le nombre de résultats et mène à une surévaluation des p-values. Nos résultats sont donc biaisés.
Fig.7 : Schéma représentant le chevauchement. Deux gènes étant régulés par le même motif.
Conclusion:Nous obtenons un résultat intermédiaire sensé et prometteur. Mais nos valeurs de p étant biaisées, notre analyse mérite d'être réitérée de manière plus rigoureuse.
Perspectives:Pour la suite, il est nécessaire de prendre en compte cet effet de chevauchement pour ne compter qu’une fois les motifs et ainsi pourvoir appliquer une correction de Bonferroni, l’analyse correspondant cette fois au modèle de la distribution hypergéométrique. Il est donc important de nettoyer de manière plus rigoureuse les données avant l’analyse.
Superviseurs: Aurelien Mace & David Lamparter
Étudiantes:Sabine Mentha, Emmanuelle Besson et Dehlia Chevalley
Présentation:PREZI [[1]]
Références: Librairie KEGG, http://www.genome.jp/kegg/ , [site web], consulté le 30.05.2013 Circuitry and Dynamics of Human Transcription Factor Regulatory Networks, Shane Neph et al., cell 150,p.1274-1286, 14 septembre 2012 An expansive human regulatory lexicon encoded in transcription factor footprints, Neph et al,Nature,2012
Back to UNIL BSc course: "Solving Biological Problems that require Math 2013"