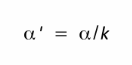Pathway enrichment in DNAse1 footprinting data

Background: Il est essentiel pour le domaine de la génétique d’éclaircir le réseau de transcription qui est impliqué dans les cellules humaines. Actuellement, des données couvrant une grande partie du génome sont accessibles au public et permettent alors une réelle avancée dans la compréhension de la régulation de la transcription.

Goal: Le but du projet était d’identifier des motifs spécifiques qui se retrouvent dans certaines voies biologiques (pathways) en cartographiant des réseaux des facteurs de transcriptions (TF). Nous souhaitions donc savoir quels TF sont impliqués dans quelles voies. Ces résultats pourraient ensuite servir d'outils pour, par exemple, identifier des dysfonctionnements dans une voie particulière ou augmenter les connaissances concernant les interactions TF-pathways.

Mathematical tools: Pour la création et la gestion de nos bases de données, nous avons utilisé le programme SQLite, qui permet la mise en lien très efficace de nombreuses tables entre elles. Pour la mise en place de requêtes et tests statistiques, nous avons opté pour le programme libre R. Le test statistique est basé sur une distribution hypergéométrique (loi des tirages sans remise). Nous avons par ailleurs essayé de corriger pour les tests multiples (Bonferroni).

Fig.1 : Calcul de la p-value avec distribution hypergéométrique.

Fig.2 :Permet d’ajuster la p-value lors de test multple.

Le seuil de rejet α <5% pour compenser le nombre de tests (k). 

Results

Conclusion

Supervisors: Aurelien Mace & David Lamparter

Students:Sabine Mentha, Emmanuelle Besson et Dehlia Chevalley

Presentation:[[1]]

Back to UNIL BSc course: "Solving Biological Problems that require Math 2012"