Optimizing gene scores for pathway enrichment
Optimizing gene score for pathway enrichment
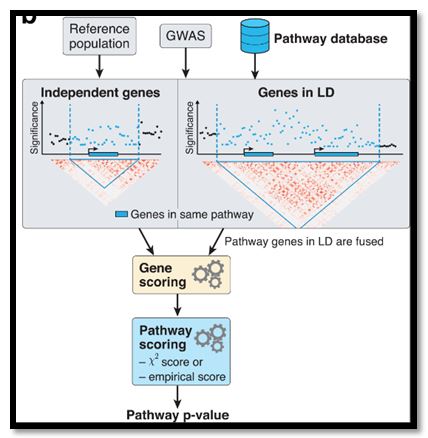
Lors de ce projet, nous avons utilisé le programme Pascal, dans le but d’affiner les critères permettant le réglage d’options souvent ignorées par les utilisateurs. Pascal est un outil permettant le calcul de gene score et de pathway score à partir de SNPs reliées à des phénotypes établis. Par « pathway » il est entendu un ensemble de gènes qui, combinés, mènent à un phénotype particulier, par exemple une maladie ou un trait physique. L’application de ces calculs de scores à grandes échelles et sur des données provenant de bases de données, ou d’études à larges échelles, comme BIOCARTA ou GWAS permettent donc de se donner une idée des processus biologiques impliqués dans la formation de phénotypes particuliers.
Le « gene score » s’établis comme suit : il s’agit premièrement d’affecter les SNPs des données étudiées, situées dans un intervalle de paires de bases en amont ou en aval du gène qui peut être définit par le biais d’options, aux gènes. Le calcul s’opère alors en quelques étapes, à commencer par celui du « z-score » puis celui du Tsum (SOCS) selon Tsum= ∑i(zi^2) . A noter que de nombreuses méthodes ont été développées pour intégrer les statistiques obtenues avec les SNPs aux « gene score », celle du SOCS consiste à combiner les résultats pour toutes les SNPs dans une région d’un gène. Nous utilisons une population de référence pour estimer la structure de corrélation entre les « z-scores » (« Statistique qui permet de conclure à la significativité ou non d'un écart dans un profil. ») et les valeurs d’SNPs d’association. Sous l’hypothèse nulle, il est possible de démontrer que les « z-scores » de n SNPs dans une région génique donnée peuvent être considéré comme suivant une distribution normale multivariée : z ~ Nn (0,∑) où Σ est une matrice de corrélation de génotypes. Nous possédons donc un génotype (vecteur pour une SNP) et un phénotype. Pour l’obtention du « z-score » on applique ensuite la régression linéaire afin de définir si le génotype à un impact sur le phénotype [N(0,1) (distribution normale du khi carré)] ou non.
Tandis que le calcul du « pathway score » peut être réalisé par le biais d’une approche se composant de trois étapes :
1) Les « gene score » subissent une transformation afin de suivre une distribution ciblée : les P-values des « gene score » sont classées de manière à ce que la P-value la plus faible obtienne le rang le plus élevé. La valeur du rang est ensuite divisé par le nombre de gènes + 1 afin d’obtenir une distribution uniforme.
2) Une statistique de test est calculée en sommant les scores de gènes membres de pathway et les gènes fusionnés : les valeurs de cette distribution uniforme sont alors transformées par la fonction quantile afin d’obtenir la distribution des scores des gènes.
3) Une méthode empirique ou analytique est utilisée pour évaluer si la statistique de test observée est plus élevée que prévue, c.-à-d., si le pathway est enrichit pour des gènes associés à des traits : les X2 « gene score », pour un pathway donné de taille m, sont additionnés et testés contre une distribution. Ainsi avec les P-values obtenues à la suite des calculs des « gene score » et des « pathway score » il est possible de définir si un phénotype est une conséquence des diverses SNPs observées dans les différents gènes.
Le but de notre projet se situe alors dans la définition de paramètres d’options permettant l’enrichissement optimal de ses scores. Pour ce faire nous avons utilisé deux paramètres différents pour les options « up » et « down », définissant comme cité précédemment les paires de bases en amont (up) et en aval (down) du gène, 0kb et 50kb.
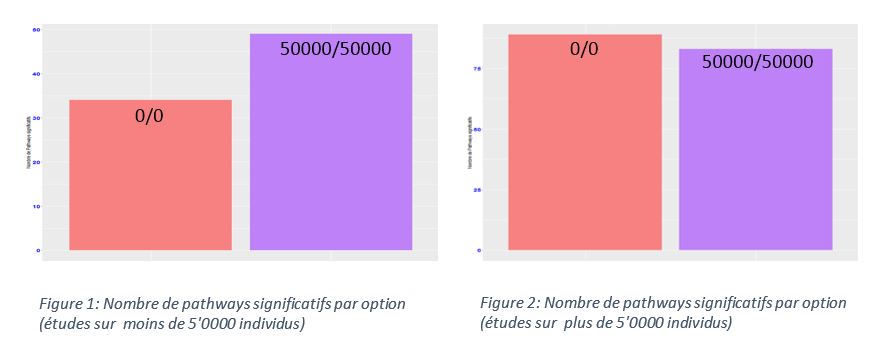
A partir de ces deux critères, avec l’aide de R, nous avons pu effectuer diverses comparaisons pour plusieurs phénotypes afin de trouver, à l’aide de barplots, si une tendance pourrait indiquer l’utilisation préférentielle d’une option. Des études de tailles variables ont été utilisées afin de démontrer l’impact de la taille de population sur le choix de l’option.
Nous avons ainsi réalisé que, pour les études portant sur plus de 50000 sujets, l’option up=0 et down = 0 montrait les meilleurs résultats. Toutefois, dans les études portant sur moins de 50000 sujets, l’option up = 50000 et down = 50000 a montré une meilleure efficacité.
Il est possible d’amener une hypothèse pour expliquer ces résultats. En cas d’étude à large échelle, le bruit de fond sera moindre et les pics de significiance beaucoup plus important. Il est donc nécessaire de n’associer au gène que les SNPs lui étant les plus proches sous peine d’ajouter des faux-positifs à nos résultats. Au contraire, dans le cas d’études à plus petite échelle, les pics de significiance seront plus restreints et plus étalés. Pour être certains de prendre en compte toutes les SNPs associés à un certain phénotype, il est nécessaire d’augmenter la fenêtre d’association gène-phénotype
En conclusion, l’option up = 0 et down = 0 semble le paramètre le plus recommandé pour les utilisateurs, lors de larges études, et ce à la place des options par défaut généralement gardée par ceux-ci. Ainsi par ce choix il sera possible d’augmenter la validité des résultats obtenus lors par exemple de recherches cliniques.
Superviseur: David Lamparter