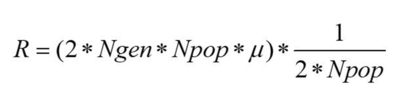Application of Wright-Fisher model for recombination landscapes

Credits

Authors: Kasandra Balzaretti, Chiara Bezzola, Milo Arigoni
Project proposed by: Diego Hartasanchez Frenk

Introduction

In population genetics, the Wright-Fisher model is used for understanding the dynamics of gene frequencies in small populations. This model illustrates how genetic drift—a mechanism characterized by random fluctuations in allele frequencies due to chance events—drives evolutionary changes. In this model also the effect of mutation can be considered. Mutations introduce new alleles into the gene pool, thereby enhancing genetic diversity over generations.
However, genetic drift and mutations are not the only factor influencing genome evolution. Recombination also plays a crucial role. Recombination is a genetic process where DNA sequences are shuffled, leading to new combinations of alleles. The probability of recombination between two genes depends on their physical distance on the chromosome; genes that are farther apart are more likely to undergo recombination compared to those that are closer together. This can result in regions of the genome that tend to remain together more frequently than would be expected by chance, a phenomenon known as linkage disequilibrium (LD). LD is the non-random association of alleles at different loci.
Understanding LD has significant applications in the medical field. By analyzing LD patterns, researchers can pinpoint genome regions associated with diseases, allowing them to identify specific genetic elements that contribute to these conditions. This knowledge is crucial for evaluating genetic risk factors and supports personalized medicine approaches. The importance of studying linkage disequilibrium in medical research strongly motivates our project.
Additionally, we explore the concept of the recombination landscape, which refers to the variation in recombination rates across different regions of the genome. Not all genomic regions experience the same recombination rate; some regions, known as hotspots, exhibit higher recombination rates, while others have lower rates. This variation has profound implications for LD. In high recombination rate regions, frequent gene shuffling reduces LD, whereas in low recombination rate regions, genes tend to remain linked, sustaining higher LD levels.

In our project we decide to simulate 3 different model of recombination landscapes.
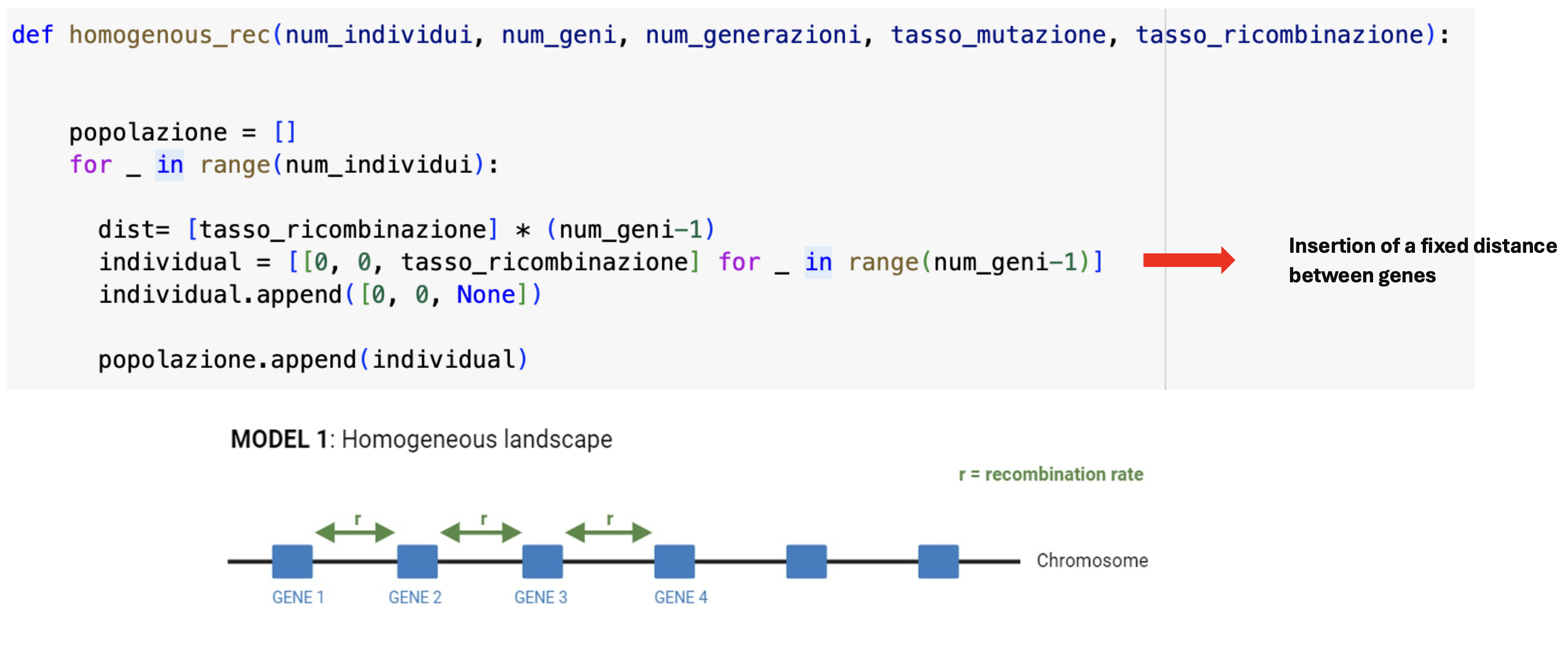
In the first one we decide to keep a homogeneous recombination rate between all the genes in each chromosome. That means that we have the same distance between all the genes.
In the second model, we attribute a random recombination rate value from a normal distribution for each intergenic space.
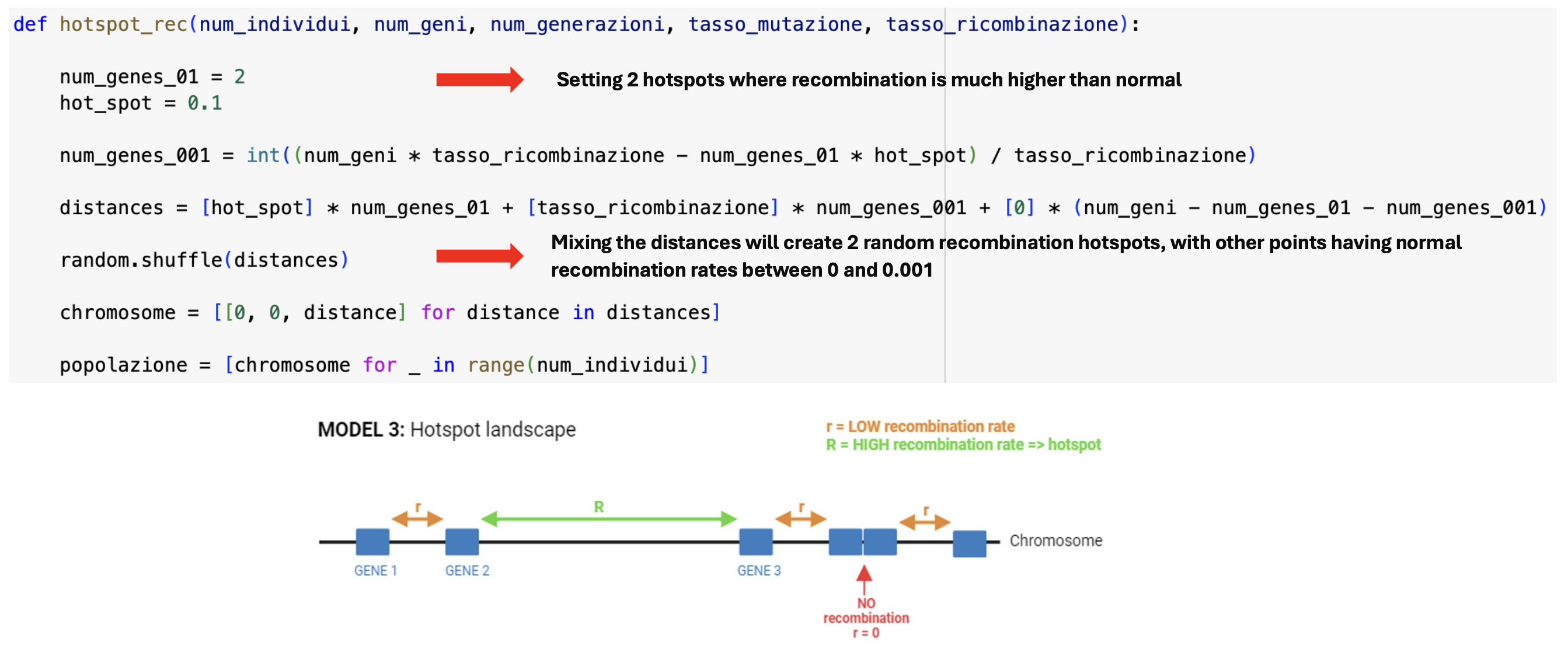
And for the last one, we chose a number of hotspots, like 2 or 3, to which we assign a high recombination rate, and then we determine a number of genes to which we will assign a lower recombination rate, and the rest of the genes will not recombine, so recombination rate equal to zero. And the number of genes with lower recombination rate will be chose in a way to have the average recombination rate per individual per generation for the 3 models to be the same. In our case it is fixed to 0.001.

Landscapes

Model Assumptions

For our model, we made several key assumptions to simplify the complexities of genetic dynamics:

1. Fixed population size and non-overlapping generations: we assume that the population size remains constant, and generations do not overlap. This means that the entire population is replaced by their offspring in each new generation
2. Random sampling of genes: we assume that allele frequency fluctuations are only due to the random sampling of genes from one generation to the next
3. Homogeneous Starting Population: initially, the population is homogeneous, with all individuals possessing the same alleles for each gene
4. Random mating, fixed mutation rate, and single crossover per chromosome
5. No Selection

Additionally, we incorporate the infinite allele model as our final assumption. According to this model, each mutation in a gene produces a new and unique allele that did not previously exist in the population. In our scenario, we begin with a homogeneous population where all individuals have the same allele (allele 0) for each gene. For instance, if four mutations occur, four new alleles will be created. The first mutation will generate allele 1, the second mutation allele 2, and so forth, using a sequential labelling system to track these mutations.

Algorithm

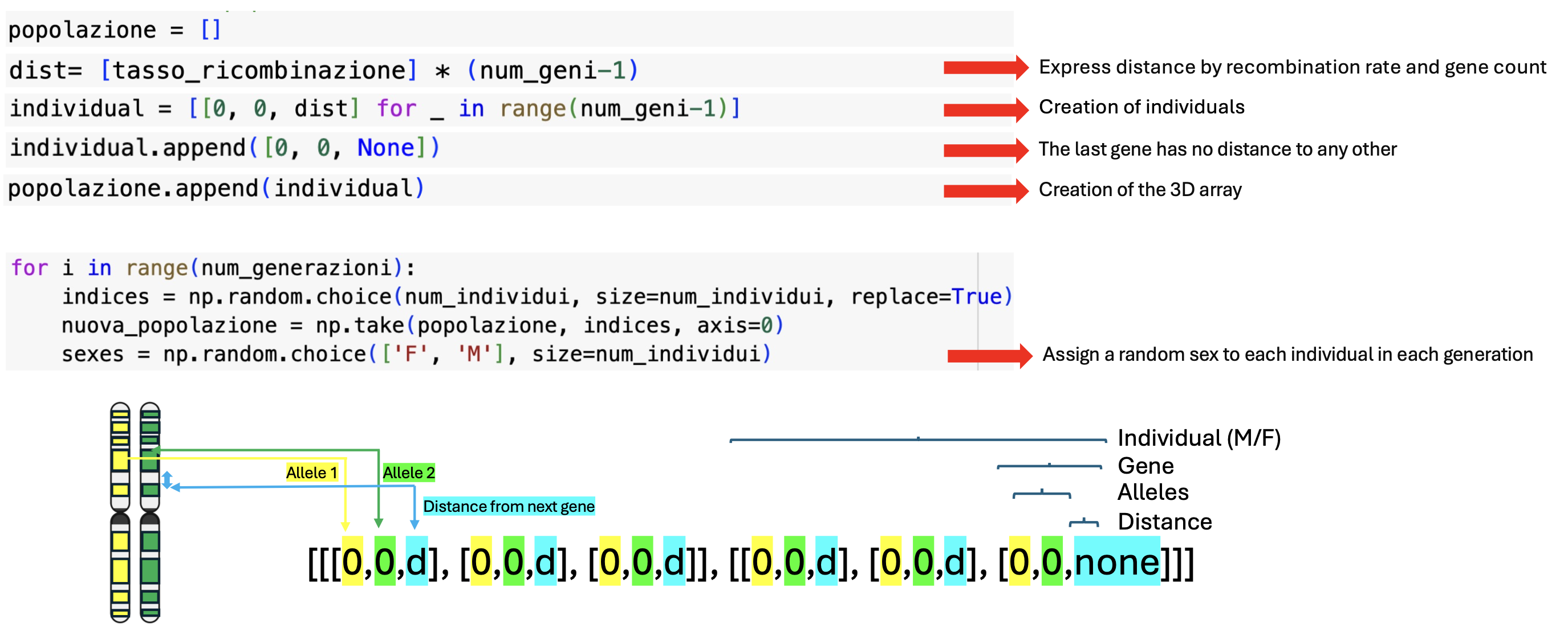
Creation of the population

Define Individuals in the Population:

• Create Population: Generate individuals for the simulation.
• Express Gene Distances: Distances are expressed based on recombination rates and the number of genes.
• Assign Alleles: Assign 0 for the ancestral allele to distinguish them from new ones.
• Distance Assignment: The last gene has no distance since distance is defined as the space from the next gene.
• 3D Array Creation: Create a 3D array where the three indexes represent the individual, gene, and either allele or distance.
• Random Sex Assignment: Each individual is assigned a random sex, allowing recombination only between different sexes.

Additionally, in the array that includes alleles and distances, each allele at position 0 represents the version on the first homologous chromosome, and the allele at position 1 represents the allele on the second homologous chromosome. Distances are measured as the distance from the next gene. In this example, we are analyzing two individuals with three genes each.

Recombination Models

Random Recombination Model:

• Simulation: Simulate a random recombination rate following a normal distribution.
• Parameters: Define the mean recombination rate and standard deviation.
• Distance Assignment: Assign distances proportional to the recombination rate and compute the model accordingly.

Homogeneous Recombination Model:

• In the homogeneous recombination model, we apply a fixed recombination rate, meaning a fixed distance between every gene.

Hotspot Recombination Model:

• The hotspot model involves defining two hotspots with recombination rates a hundred times higher than the others due to their significant intergenic spaces.
• The distances are then randomly shuffled and assigned to random intergenic spaces.

Detailed Recombination Simulation

Analyzing the recombination simulation in detail:

• Iteration: Iterate over each individual, giving them the possibility to recombine in each generation.
• Sex Determination: Determine sex based on the previously created sex array.
• Exclusion of Last Gene: Exclude the last gene from recombination.
• Distance Conversion: Convert distances into recombination rates (probability of being chosen) since they are proportional.
• Recombination Probability: Choose intergenic spaces to recombine based on probabilities.
• Partner Selection: Select a random partner of the opposite sex for recombination.
• Allele Selection: Randomly select which allele to recombine and perform recombination by exchanging all genes downstream of the selected one between two individuals.

Calculating Linkage Disequilibrium

We created a function to calculate linkage disequilibrium:

• Mutation List: Define a list of all mutations in the last generation representing different alleles.
• Dictionary Creation: Create a dictionary to assign an index to each mutation for later use in the matrix.
• Matrix Building: Construct an empty matrix to store the data.
• Iteration and Counting: Iterate over each chromosome, counting the co-occurrence of each mutation with all others.
• D Value Calculation: Calculate the D value for each pair of alleles based on co-occurrence to understand their linkage.

Results and discussion

Before studying the LD we tested our model on different theoretical expectations of the Wrigh-Fisher model.
To test our model we decided to use values that could reflect the reality as much as possible. So we fixed the population size at 200 individuals and we looked at its evolution for 1000 generations. Then we decided that each chromosome would have 2000 genes. This value was based on the Drosophila genome and corresponds to the mean number of genes per chromosome divided by two. In addition, we fixed the mutation rate at 0.0001 - which corresponds to the mutation rate per allele in humans - and the recombination rate at 0.001 - which is the mean recombination rate per chromosome in Drosophilae.

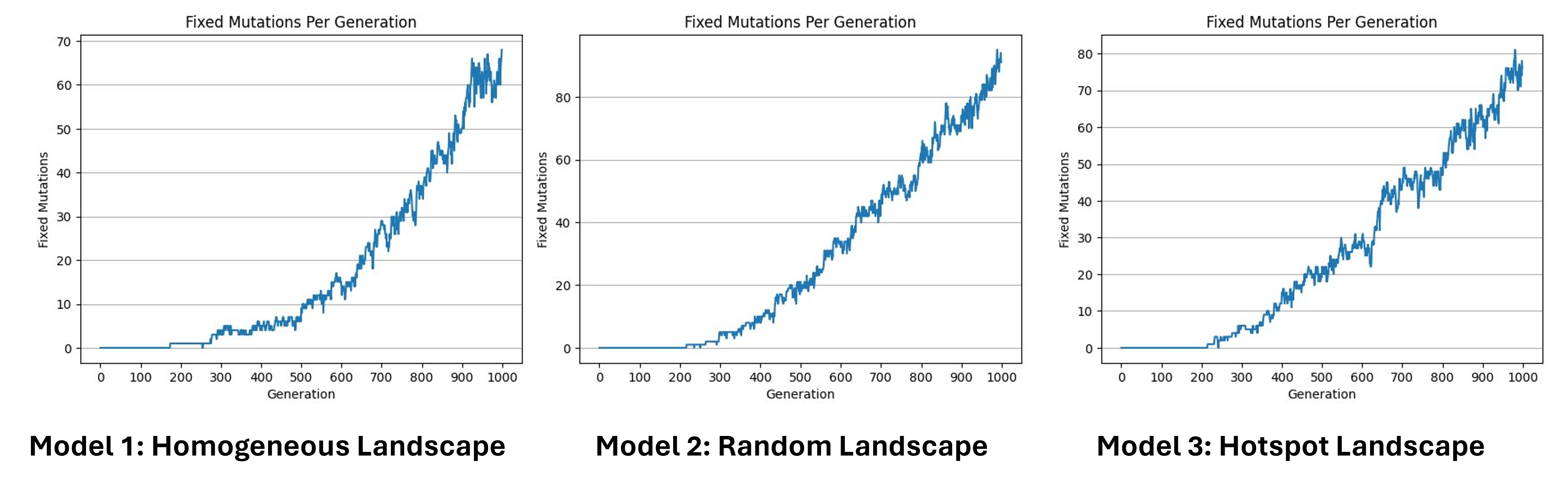
Fixed mutations per generation

Hear we can see the number of fixed mutations per generation. As we said before, a mutation is fixed when, for a specific gene, all individuals of the population are homozygote for this specific mutated allele, which means that its frequency has reached 100%. Here we can see that the increase is not linear, in some cases the fixed mutations are lost. This can be caused by a second mutation that happened in the same allele, by recombination, or can be simply the source of genetic drift. Since we have no selection we can estimate the number of fixed mutations per generation by multiplying the number of expected new mutations per generation by the probability of fixation, which is approximately 1/2N.

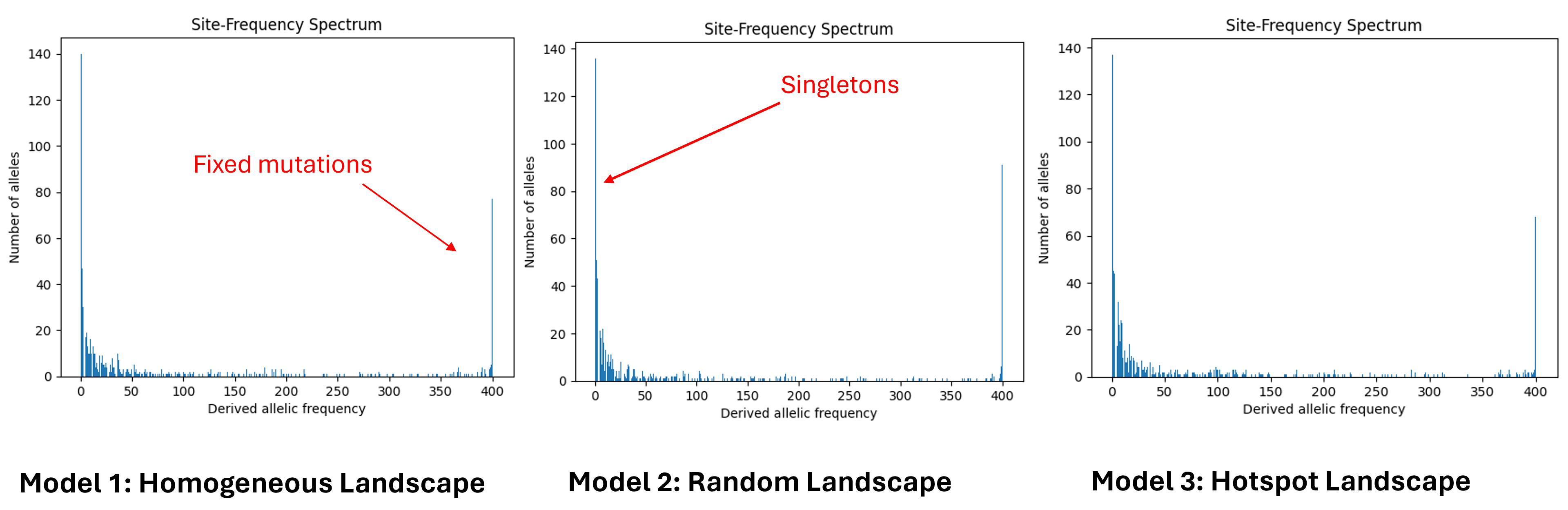
Site Frequency Spectrum (SFS)

Site Frequency Spectrum (SFS) summarizes the allele frequency distribution by counting the number of sites at each allele frequency. Here, the x-axis shows allele frequency categories, and the y-axis shows the count of sites in each category. At equilibrium, the SFS typically follows a 1/x distribution, where x is the frequency. In all three models, most alleles appear in one copy as singletons. The last peak represents fixed mutations, which are alleles with a frequency of 100%. In all the models we obtain the expected distribution:

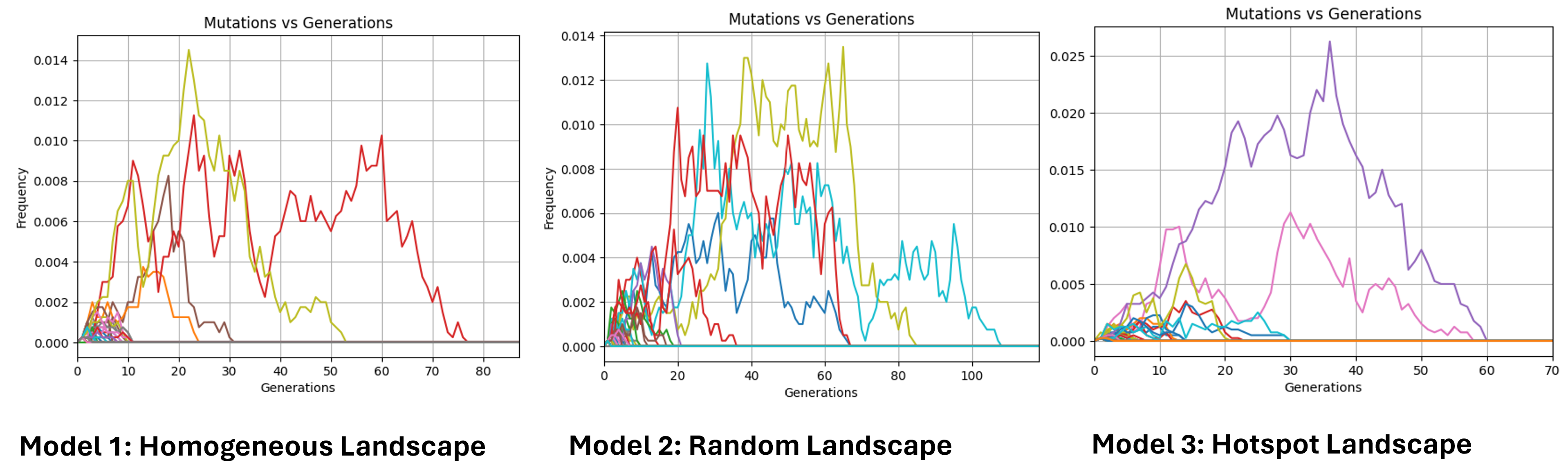
Alleles frequencies fluctuations

Hear we trace the frequency of randomly selected mutated alleles across a selected window of time. A new mutation in a diploid population of size N starts with the following frequency:

Due to genetic drift, new mutations, and recombination, some alleles disappear quickly, while others persist longer.

Recombination landscape and Linkage disequilibrium

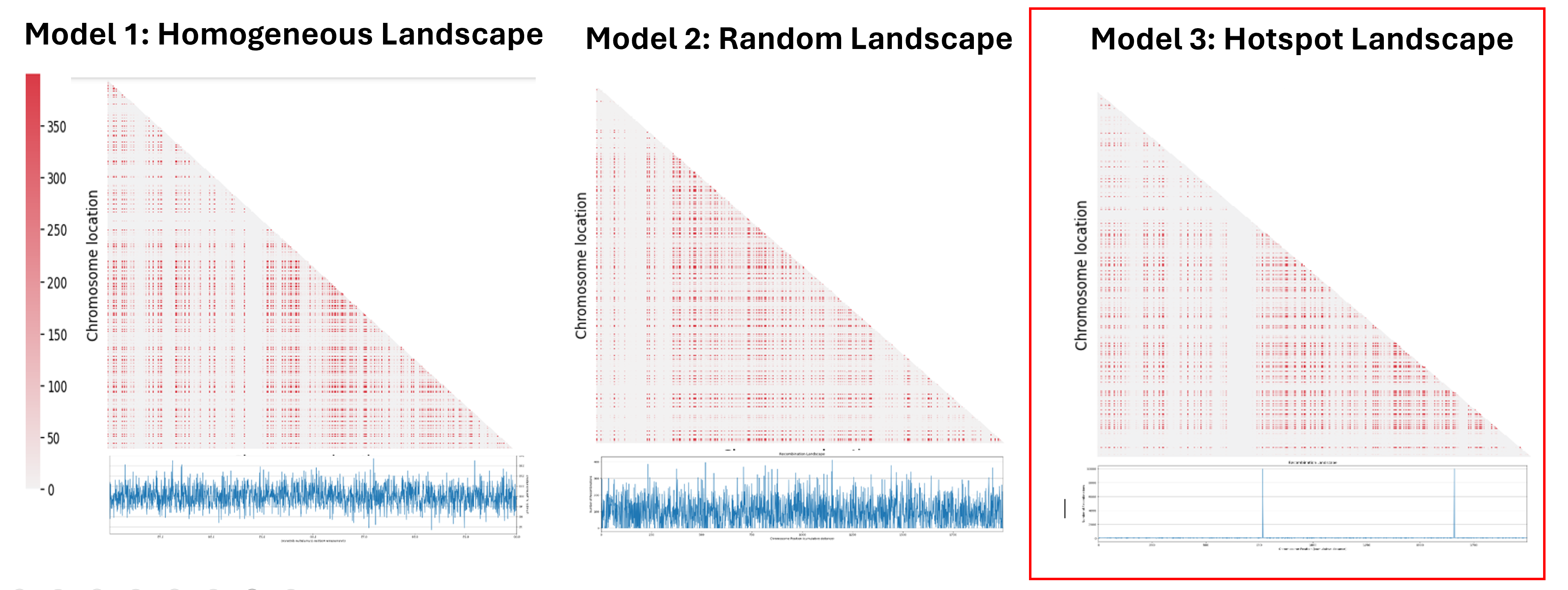
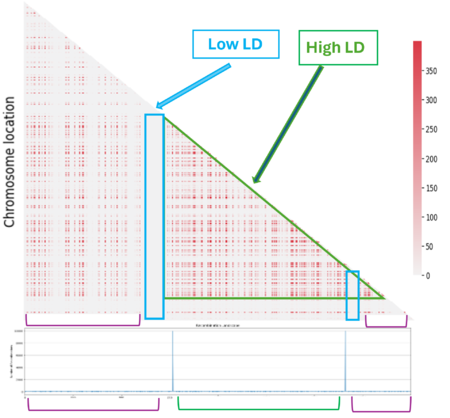
The next step was to understand the impact of the recombination landscape on linkage disequilibrium. To do that we have calculated parameter D, which quantifies the non-random association of alleles, and then used it to represent the result with a heatmaps where the more red the region is, the more associated the genes are. In this case only the last generation of the simulation was represented. We then analyzed the heatmaps for the homogenous recombination landscape since the recombination is homogenous is the same for all intergenic regions, we didn’t notice any particular pattern, and so there is no formation of LD regions. We can draw a similar conclusion for the random landscape model: in fact, even if the recombination rate is non homogenous, it is distributed homogenously across the chromosome, not allowing the formation of particular LD regions. However, in the hotspot landscape, a distinct LD regions is formed, so we decided to focus our analysis on this model.

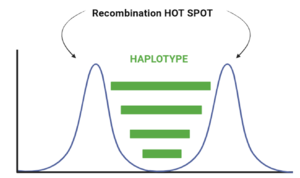
When we look at the Hotspot landscape, we can clearly identify 2 regions: the one highlighted in green, which is localized between the two hotspots and is characterized by high linkage disequilibrium, and the one in blue, which represents the within hotspot regions and shows a zero linkage disequilibrium. In fact, high recombination breaks down LD within the hotspot. On the other hand, the regions between hotspots tend to have lower recombination rates. Consequently, the alleles in these regions are less shuffled and often remain linked over generations. These regions are called haplotypes:

Improvement of the results

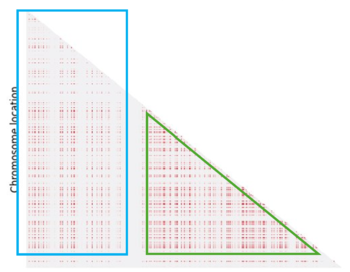
Even if we can identify a pattern, it doesn't fully meet our expectations. In fact we expected to see more LD regions (in light blue) and the one we have identified is not clearly defined (in green):

This could be due to three main factors:

• Mutations and genetic drift introduce noise and disrupt linkage between genes
• The absence of selection allows more fluctuation in the allelic frequencies and consequently prevents the complete fixation of linkage between genes
• We used only the last generation to create the heatmaps, and so there is a possibility that we have lost some information that were present in the previous generations

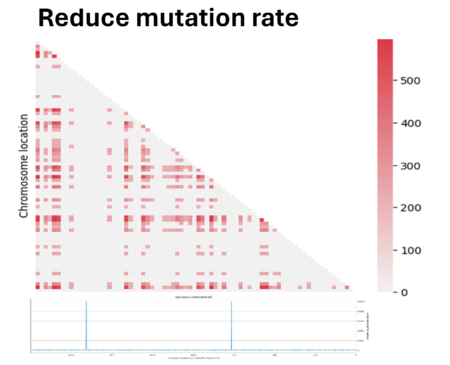
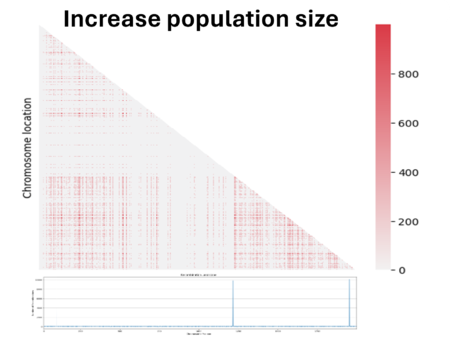
So we tried to play a bit with parameters to see if we could improve the quality. First we have reduced the mutation rate by 100. However, since we applied an infinite allele model, the reduction of mutation has led to fewer different alleles present in the population, making the population mostly homogeneous and making it difficult to measure linkage between genes. In fact most regions showed zero linkage disequilibrium.

Then we decided to also double the population size. We see here that the noise caused by genetic drift in the LD region has decreased, but at the same time the parameter D has also decreased. In fact, the bigger the population is and the more difficult it is to see the same linked genes in all individuals in the population if there are favored by natural selection.

Next steps

The next steps would be the implementation of natural selection and allelic fitness to observe how LD regions can be favored if they have a positive impact on fitness. In addition, to improve the results, we could collect LD information from multiple generations and join them in a unique heatmap.