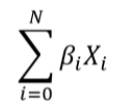Difference between revisions of "Polygenic Risk Scores"
Sbprm2021 3 (talk | contribs) |
Sbprm2021 3 (talk | contribs) |
||
| (8 intermediate revisions by the same user not shown) | |||
| Line 27: | Line 27: | ||
=='''<big>Results</big>'''== | =='''<big>Results</big>'''== | ||
| − | [[File:GWASGroup1_PRS_1.2.png | + | ='''Group 1 GWAS'''= |
| + | [[File:GWASGroup1_PRS_1.2.png]] | ||
| − | + | First in our project, we performed a PRS analysis on the GWAS study of the first group. They made a GWAS analysis that was pruned and qq-normalized. The figure above is a Manhattan plot of the group 1 result's. Using their beta effect size and at a threshold of 5 * 10^-8, we made the PRS calculations. | |
| − | + | ||
| + | [[File:GWASGroup1_PRS_2.2.png]] | ||
| − | + | But the distribution of the obtained PRS score was weird. Most of the subjects had a PRS score around -14, while only a few were distributed. This was different of the expected bell curve. Because of this we couldn't cut the data into deciles, because the data hadn't enough variation. But the separation into sextiles and quartiles showed a linked between the PRS score and the mean sextile BMI, and also between the PRS score and mean quartile age of heart attack. | |
='''Study GWAS'''= | ='''Study GWAS'''= | ||
| − | + | [[File:GWASStudy_PRS_1.2.png]] | |
| − | ( | + | Because of the weird obtained results of the PRS calculations on the group 1 GWAS, we also performed a PRS calculation on the results of a published GWAS study of 2015 (Locke et al, 2015). There is the manhattan plot of the study above. The calculated PRS score's were this time perfectly distributed normally. |
| + | [[File:GWASStudy_PRS_2.2.png]] | ||
| + | |||
| + | The scatter plot of the PRS score against BMI shows a small link between the PRS score and the BMI. When separated into deciles, we can clearly see a link between the deciles and the mean BMI score. Also, the extreme deciles of 1 and 10 are respectively more represented in the weight categories of normal and obese and severely obsese. | ||
| Line 49: | Line 54: | ||
Then on the right we looked at pretty much the same thing, but with our PRS measurement for BMI. Here again, it’s less straightforward but we see the same trend as before where the higher the PRS, so the higher the risk is, the youngest someone is to get a heart attack. | Then on the right we looked at pretty much the same thing, but with our PRS measurement for BMI. Here again, it’s less straightforward but we see the same trend as before where the higher the PRS, so the higher the risk is, the youngest someone is to get a heart attack. | ||
| − | + | [[File:Phenotypes_PRS_1.2.png]] | |
| + | |||
Finally we looked at diabetes. When plotting the age of diabetes diagnosis with PRS, we can’t quite figure out a trend and then when we plot it again against BMI we see something interesting. Here we see that the age of diagnosis comes earlier in life for both high AND low BMI. Since we can see both those ends of the plot being meaningful for age of diabetes, this might explain why when we plot it against the PRS we can’t see much and can’t tell with the PRS alone if there is a link between those 2. | Finally we looked at diabetes. When plotting the age of diabetes diagnosis with PRS, we can’t quite figure out a trend and then when we plot it again against BMI we see something interesting. Here we see that the age of diagnosis comes earlier in life for both high AND low BMI. Since we can see both those ends of the plot being meaningful for age of diabetes, this might explain why when we plot it against the PRS we can’t see much and can’t tell with the PRS alone if there is a link between those 2. | ||
| − | + | [[File:Phenotypes_PRS_2.2.png]] | |
Latest revision as of 22:51, 5 June 2021
- Project name: Polygenetic Risk Score (PRS)
- Tutor: Alex Button (alexanderluke.button_AT_unil.ch)
- Slides: File:Polygenetic Risk Score.pdf
Contents
Introduction
Definition
Polygenic Risk Score or PRS is the calculation of a risk score from the subject's genome with the weighted sum of the SNPs to estimate the risk that the subject will develop a certain disease or trait according to the changes linked to the phenotype studied. There are two main factors that we use to calculate the PRS: the allelic dosage (Xi), which represents the number of copies of the main effect allele and can be 0, 1 or 2. And the other factor is the effect size (βi), which measures the strength of the relationship of a trait with the allelic dosage at a position i on a numeric scale.
Jura & UK Biobank
In order to have data, we used Jura, which is a cluster for analysis of sensitive data and is primarily used by the CHUV. We need to have authorization to use Jura, but like that we can have real subject’s data.And there are data coming from the UK Biobank, which is a large-scale biomedical database and research resource, containing genetic and health information from half a million UK participants that is enabling new scientific discoveries to be made that improve public health.
Our goal with this project
Our goal is to compare the polygenic risk score that we found for the SNPs of the different BMI indices from group 1. And if possible make connections and correlations with diseases.
Why is Polygenic Risk Score important ?
The Polygenic Risk Score is used for disease outcome prediction. It indicates the relative risk for the disease or trait studied, compared to other people with different genomes. But we must be careful with the results, because it gives us correlations and correlations are not equal to causations. There are other factors that are not necessarily considered, such as the environment. Nevertheless it can be useful, for example: the riskiest people can be prepared and can take predispositions with their doctors. However, it will be more accurate for some people. For the moment, the use of PRS is not widespread, because there are no guidelines, and it is still in process of improvement. It will always be probabilities and not certitudes. Despite the statistics behind it, PRS could potentially be very powerful to “simply” predict (at birth) all kinds of diseases one could encounter. It is still a bit early for that, but it could help people in the future.
Results
Group 1 GWAS
First in our project, we performed a PRS analysis on the GWAS study of the first group. They made a GWAS analysis that was pruned and qq-normalized. The figure above is a Manhattan plot of the group 1 result's. Using their beta effect size and at a threshold of 5 * 10^-8, we made the PRS calculations.
But the distribution of the obtained PRS score was weird. Most of the subjects had a PRS score around -14, while only a few were distributed. This was different of the expected bell curve. Because of this we couldn't cut the data into deciles, because the data hadn't enough variation. But the separation into sextiles and quartiles showed a linked between the PRS score and the mean sextile BMI, and also between the PRS score and mean quartile age of heart attack.
Study GWAS
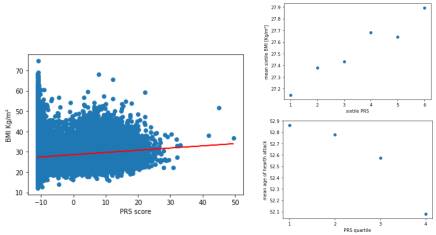
Because of the weird obtained results of the PRS calculations on the group 1 GWAS, we also performed a PRS calculation on the results of a published GWAS study of 2015 (Locke et al, 2015). There is the manhattan plot of the study above. The calculated PRS score's were this time perfectly distributed normally.
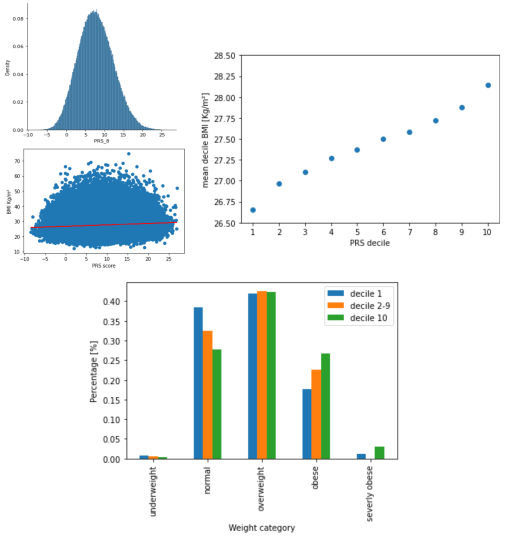
The scatter plot of the PRS score against BMI shows a small link between the PRS score and the BMI. When separated into deciles, we can clearly see a link between the deciles and the mean BMI score. Also, the extreme deciles of 1 and 10 are respectively more represented in the weight categories of normal and obese and severely obsese.
Looking into other phenotypes
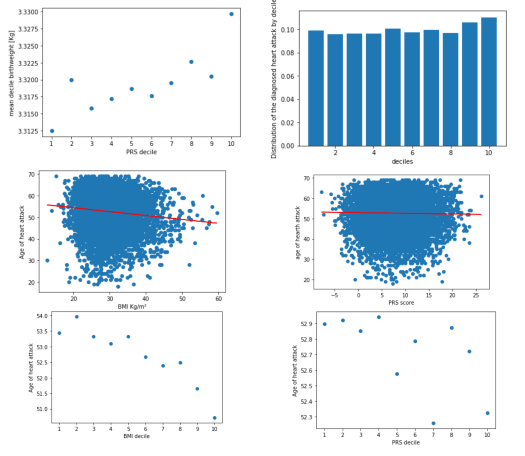
We looked at the mean weight at birth in function of our PRS for BMI. We see that birthweight is linked and increases with the PRS. What this means is that the bigger a baby is at birth, the more risks it has to become obese later in life.
We also looked at the repartition of heart attack in function of the deciles, but here the results we got didn’t show much.
We further looked into heart attack, more specifically the age of heart attack. When plotting the age of heart attack in function of BMI we can see that now we have an interesting result. The link we see here (so in the 2 plots on the left) is the higher the BMI, the earliest in age someone is to have a heart attack, which makes sense because obesity is known to be causal of cardiovascular diseases.
Then on the right we looked at pretty much the same thing, but with our PRS measurement for BMI. Here again, it’s less straightforward but we see the same trend as before where the higher the PRS, so the higher the risk is, the youngest someone is to get a heart attack.
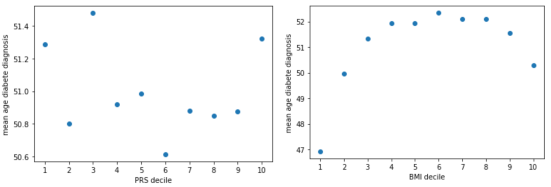
Finally we looked at diabetes. When plotting the age of diabetes diagnosis with PRS, we can’t quite figure out a trend and then when we plot it again against BMI we see something interesting. Here we see that the age of diagnosis comes earlier in life for both high AND low BMI. Since we can see both those ends of the plot being meaningful for age of diabetes, this might explain why when we plot it against the PRS we can’t see much and can’t tell with the PRS alone if there is a link between those 2.
Conclusion
Back to our goal and question
Our initial plan for the project was to do a PRS on the BMI results made by group 1. We wanted to look at different PRS results from their different BMI indexes and potentially get interesting results. The issue we got is that when we did our first analysis for their default BMI index, it wasn't the expected results. We then tried for the other indexes but there again the PRS distribution wasn’t as good as expected. We were not sure why that was the case, it could either be an issue with the data, like how it was collected, the threshold used ... or it could’ve simply been due to our code that was doing something wrong.
To better understand what was going wrong we took data from an already published study that basically did the same thing we were trying to do, and did a polygenic risk score on it. As you just saw, it worked fine so our code was not the issue. Now, we still don’t know why it didn’t work before but we still had to complete our analysis, for that we still made use of the results from group 1 as well as the ones from the published study.
To answer our question of "Can PRS be used to predict disease outcome?", we used the Pearson correlation as a predictive measurement. We found 6.1% for group 1 and almost 9% for the study. These don’t look that high but when comparing to what the published study found, that is 10.4%, it’s actually quite close. So our analysis using PRS was quite accurate to predict disease outcome.
Take home messages
Using PRS we looked at multiple phenotypes and how they correlate. We saw that for example weight at birth, age of heart attack and even age of diabetes diagnosis is linked to higher BMI.
More generally, with polygenic risk score we are able to simply and easily predict diseases. We mostly focused on BMI but PRS can also be used to predict other complex diseases like coronary artery disease and that by simply looking at DNA, and removing the need to do tedious or invasive conventional tests for such diseases.
Another good and practical aspect of PRS is that unlike other methods, we can predict diseases without knowing the specific genes affected. Only by using the SNPs and the GWAS studies of course, we can tell if someone is at risk of developing a certain disease or phenotype without the knowledge of the genes affected.
Let’s not forget though that it is still a developing method that doesn’t quite have a strong predictive value like we showed with our analysis, and also the fact that it’s only quite accurate for European ancestries. So, being able to use it worldwide won’t happen anytime soon.
References
Contacts
Morgane Bovard (morgane.bovard@unil.ch)
Antonio Garrido Marques (antonio.garridomarques@unil.ch)
Didier Markwalder (didier.markwalder@unil.ch)
Teaching assistant : Alex Button (alexanderluke.button@unil.ch)