Difference between revisions of "Modeling: Pattern formation using Reaction-Diffusion models"
| Line 27: | Line 27: | ||
---- | ---- | ||
(Project in [[Course: "Solving Biological Problems that require Math"]]) | (Project in [[Course: "Solving Biological Problems that require Math"]]) | ||
| + | |||
| + | |||
| + | == Développement de notre projet == | ||
| + | |||
| + | I. Introduction | ||
| + | |||
| + | 1.1 Notre sujet | ||
| + | |||
| + | Qui ne s'est jamais poser la question: pourquoi un zèbre est-il rayé? On pourrait répondre par la théorie de l'évolution en affirmant que les rayures offrent un meilleur camouflage et donc une valeur adaptative supérieur. Par contre on pourrait aussi se poser la question: comment un zèbre obtient-il ses rayure? Ici, on voit qu'il faut répondre à la question de manière moléculaire. | ||
| + | |||
| + | Le modèle d'Allan Turing (article écrit en 1952) affirme que l'interaction entre certaines molécules amène la " surface " du zèbre à se différencier en fonction des concentrations de chacune des dites molécules. Dans ce modèle, on trouve un activateur et un inhibiteur où la présence de l'activateur induira la production de l'inhibiteur tandis que la présence de l'inhibiteur induira la destruction de l'activateur. En gros; plus il y a d'activateur, plus il y a d'inhibiteur, moins il y a d'activateur, moins il y a d'inhibiteur, plus il y a d'activateur... et tout ce joli manège jusqu'à ce qu'il y aie stabilisation des concentrations moléculaire et donc, si on est pas trop malchanceux, formation d'un motif. | ||
| + | |||
| + | Affin de comprendre ce processus, il nous faudra utiliser les équations différentielles qui nous permettent de mettre en interaction plusieurs paramètres simultanément (concentrations, position, temps). Pour ce faire, on utilisera un logiciel de traitement de matrice: Matlab. | ||
| + | |||
| + | 1.2 Principes de base des équations différentielles : petite histoire d'une population (semaine 3) | ||
| + | |||
| + | Pour comprendre les équations différentielles, prenons un exemple intuitif, la dynamique d'une population. Le taux de variation du nombre d'individus d'une population est soumis à deux facteurs: le taux de natalité et le taux de mortalité, et c'est la somme de ces deux taux qui donnera la variation du nombre d'individus à chaque génération. Si ce taux est positif, la taille de la population augmentera à l'infini et s'il est négatif, la taille de la population diminuera jusqu'à disparition. | ||
| + | |||
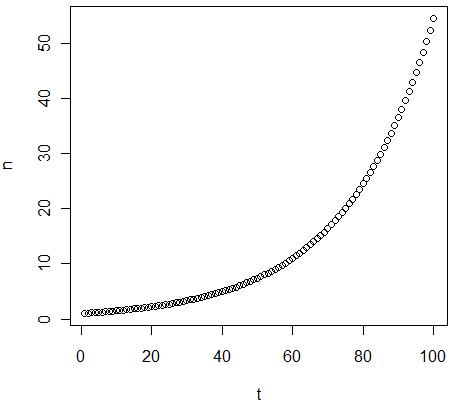
| + | Mais évidemment, le taux de natalité et de mortalité dépendent de la taille de la population. En effet, plus il y a d'individus, plus il y a de nouveaux-nés et de décès. Considérant ceci, nous pouvons aisément comprendre que si le taux de variation est positif, plus la population sera grande, plus sa taille augmentera rapidement et au contraire si le taux de variation est négatif : plus la population sera grande plus sa taille diminuera vite. | ||
| + | |||
| + | [[Image:graph1.jpg]] | ||
| + | |||
| + | |||
| + | Nous pouvons aussi remarquer qu'il existe des points où la taille de la population reste stable. Ces points sont appelé point fixe. Parmi ces points fixes, il y a la solution triviale où le taux de variation est nulle et donc la taille de la population ne change pas. Mais il existe des points fixes plus intéressant où malgré un taux de variation non nulle, la taille de la population reste stable. Ces points stables sont les endroits où, étant une taille de population donnée, le taux de natalité compense exactement le taux de mortalité. Ce point fixe peut avoir deux états : instable ou stable. En effet, avec un taux de variation positif, aussitôt que la taille de la population s'écarte légèrement de ce point, on assistera à une augmentation de la population et on ne retournera pas au point fixe. Nous qualifions donc ce point d'instable. Au contraire, avec un taux de variation positif, la population pourra avoir n'importe quel taille, elle tendra toujours à diminuer et à atteindre le point fixe et, une fois atteint, à ne plus bouger (stable). | ||
| + | |||
| + | |||
| + | |||
| + | Ce modèle simple peut aussi s'appliquer à d'autres type de courbe (parabolique, logarithmique, etc), le nombre et l'état des points fixes étant déterminés par comment la courbe coupe l'axe des x. | ||
| + | |||
| + | Dans notre projet, on s'intéressera à un modèle de diffusion-réaction où ce ne sera plus la taille d'une population qui variera en fonction d'elle même mais la concentrations de deux molécules en fonction de leur position sur une surface et des concentration respective des dites molécules. | ||
Revision as of 07:56, 29 May 2009
Background: One of the most amazing properties of biological systems is their ability to form complex and organized structures. Those structures range from simple patterns (like the stripes of a zebra) to highly complex constructs (like a cell). How such structures or patterns can emerge by themselves remains a largely unsolved problem. In this project, we investigate how a simple pattern can emerge in a decentralized manner, without any plan.
Goal: The goal of the project is to understand and analyze (with computer simulations) one of the simplest and most influential pattern formation mechanism using Reaction-Diffusion models.
Mathematical tools: This project uses partial differential equations. A short introduction to partial differential equations will be provided. A mathematical software for performing simulations (matlab) will also be used.
Biological or Medical aspects: It will be investigated to which extend this model can explain the patterns observed on animals such as leopards or zebras.
Supervisor: Micha Hersch
Presentation: Media:Micha.ppt
Students: Christophe Seppey and Balazs Laurenczy
References:
The pioneering paper from Alan Turing <biblio>
- turing53chemical pmid=2185858 pdf file
</biblio> A short treatment in, Farkas, Dynamical Models in Biology, Academic Press, 2001 Media: FarkasA3.3.pdf
Mathematical background
See the Introduction to dynamical systems and differential equations Media: FarkasA3.3.pdf
(Project in Course: "Solving Biological Problems that require Math")
Développement de notre projet
I. Introduction
1.1 Notre sujet
Qui ne s'est jamais poser la question: pourquoi un zèbre est-il rayé? On pourrait répondre par la théorie de l'évolution en affirmant que les rayures offrent un meilleur camouflage et donc une valeur adaptative supérieur. Par contre on pourrait aussi se poser la question: comment un zèbre obtient-il ses rayure? Ici, on voit qu'il faut répondre à la question de manière moléculaire.
Le modèle d'Allan Turing (article écrit en 1952) affirme que l'interaction entre certaines molécules amène la " surface " du zèbre à se différencier en fonction des concentrations de chacune des dites molécules. Dans ce modèle, on trouve un activateur et un inhibiteur où la présence de l'activateur induira la production de l'inhibiteur tandis que la présence de l'inhibiteur induira la destruction de l'activateur. En gros; plus il y a d'activateur, plus il y a d'inhibiteur, moins il y a d'activateur, moins il y a d'inhibiteur, plus il y a d'activateur... et tout ce joli manège jusqu'à ce qu'il y aie stabilisation des concentrations moléculaire et donc, si on est pas trop malchanceux, formation d'un motif.
Affin de comprendre ce processus, il nous faudra utiliser les équations différentielles qui nous permettent de mettre en interaction plusieurs paramètres simultanément (concentrations, position, temps). Pour ce faire, on utilisera un logiciel de traitement de matrice: Matlab.
1.2 Principes de base des équations différentielles : petite histoire d'une population (semaine 3)
Pour comprendre les équations différentielles, prenons un exemple intuitif, la dynamique d'une population. Le taux de variation du nombre d'individus d'une population est soumis à deux facteurs: le taux de natalité et le taux de mortalité, et c'est la somme de ces deux taux qui donnera la variation du nombre d'individus à chaque génération. Si ce taux est positif, la taille de la population augmentera à l'infini et s'il est négatif, la taille de la population diminuera jusqu'à disparition.
Mais évidemment, le taux de natalité et de mortalité dépendent de la taille de la population. En effet, plus il y a d'individus, plus il y a de nouveaux-nés et de décès. Considérant ceci, nous pouvons aisément comprendre que si le taux de variation est positif, plus la population sera grande, plus sa taille augmentera rapidement et au contraire si le taux de variation est négatif : plus la population sera grande plus sa taille diminuera vite.
Nous pouvons aussi remarquer qu'il existe des points où la taille de la population reste stable. Ces points sont appelé point fixe. Parmi ces points fixes, il y a la solution triviale où le taux de variation est nulle et donc la taille de la population ne change pas. Mais il existe des points fixes plus intéressant où malgré un taux de variation non nulle, la taille de la population reste stable. Ces points stables sont les endroits où, étant une taille de population donnée, le taux de natalité compense exactement le taux de mortalité. Ce point fixe peut avoir deux états : instable ou stable. En effet, avec un taux de variation positif, aussitôt que la taille de la population s'écarte légèrement de ce point, on assistera à une augmentation de la population et on ne retournera pas au point fixe. Nous qualifions donc ce point d'instable. Au contraire, avec un taux de variation positif, la population pourra avoir n'importe quel taille, elle tendra toujours à diminuer et à atteindre le point fixe et, une fois atteint, à ne plus bouger (stable).
Ce modèle simple peut aussi s'appliquer à d'autres type de courbe (parabolique, logarithmique, etc), le nombre et l'état des points fixes étant déterminés par comment la courbe coupe l'axe des x.
Dans notre projet, on s'intéressera à un modèle de diffusion-réaction où ce ne sera plus la taille d'une population qui variera en fonction d'elle même mais la concentrations de deux molécules en fonction de leur position sur une surface et des concentration respective des dites molécules.