Difference between revisions of "Top-bottom differences in retinal vascular properties"
| Line 33: | Line 33: | ||
A more precise way separation would be to use anchor points within the retina graph, such as the position of the fovea and the optical disc. we could then draw a line and consider again, everything above belonging to the top etc. But we still have a problem, because vessels are intertwined meaning that some bits from one side will cross over the line and we wrongly attributed. | A more precise way separation would be to use anchor points within the retina graph, such as the position of the fovea and the optical disc. we could then draw a line and consider again, everything above belonging to the top etc. But we still have a problem, because vessels are intertwined meaning that some bits from one side will cross over the line and we wrongly attributed. | ||
| + | [[File:Capture d’écran 2024-05-31 à 11.23.50.png|thumb]] | ||
| − | |||
| − | Once we have this list of segments belonging to the top or the bottom for both the arteries and the veins, we can compute the tortuosity of each segment, and extract values such as the median tortuosity for the top/bottom and for the veins/arteries. | + | To account to this, we took the connected components of the graphs, and calculated their barycentres. Their barycentres are the centers of the clusters. So it's a majority vote, and instead of deciding if the points are above or below the line, we decide if the cluster centres are above or below the line, then we attribute the rest of the cluster points to the orientation of the cluster center, and it is more likely to be accurate. This is the method we used for the final calculation. |
| + | |||
| + | Once we have this list of segments belonging to the top or the bottom for both the arteries and the veins, we can compute the tortuosity of each segment, and extract values such as the median tortuosity for the top/bottom and for the veins/arteries. We will also calculate the asymmetry coefficient with the following formula: Tau = \frac{tort_top - tort_bottom}{tort_top + tort_bottom}. The absolute value can be sometimes computed but then the orientation of a potential asymmetry is lost because without it we know that if the asymmetry is positive, the tortuosity of the top hemisphere is higher than the one at the bottom. We added a control to see if there is a real difference between top and bottom: we randomly attributed 'top' or 'bottom' to all of the vessels segments and calculated then the top and bottom tortuosity of those random hemisphere to compare it with the distribution of the asymmetry when top and bottom is attributed according to the real position of the vessel in the retina. | ||
After producing a dataframe of the new values, we switched to R for the statistical analysis. | After producing a dataframe of the new values, we switched to R for the statistical analysis. | ||
| Line 42: | Line 44: | ||
==Results== | ==Results== | ||
| − | One other way of looking if the tortuosities are similar on the top/bottom to the global one, we can make linear regression models between the global tortuosity for arteries/veins and each regional tortuosity (top/bottom). | + | One other way of looking if the tortuosities are similar on the top/bottom to the global one, we can make linear regression models between the global tortuosity for arteries/veins and each regional tortuosity (top/bottom). We obtained coefficients of determination in the 0.6~0.75 range, suggesting a correlation, but not of 1, meaning that there is information in this half retina that is specific to it and that the global tortuosity cannot fully explain. One alternative hypothesis could be that when we plot the top tortuosity against the global tortuosity we lack half of the information to make the comparison which is the other half of the retina therefore we cannot explain the variance fully but if the tortuosity were equivalent between the top and the bottom, this "representative half" would be a much better estimator. We could still randomise the segments for the top/bottom tortuosities and see if we find the same values. If we do, then the low R² is because we lack values and if we don't it's because the information in the top/bottom section is specific to it. So when randomized, the R² become considerably higher compared to the non-randomized in the 500 retina sample. This means that still with half the data, we are able to explain the global tortuosity much better. The fact that it does not go higher is probably because the sample is not large enough (we did it on the 500 retinas and not the 10'000). Proportion of the variance of TOP/BOTTOM tortuosity (variable Y) explained by global tortuosity (variable X independent) is between 60-70%. This means that the overall tortuosity of the veins/arteries explains a large proportion of the variance observed in the tortuosity of the veins/arteries in the top or bottom hemisphere, although it is not a complete explanation. |
| − | + | So this measure is not 100% redundant and we can consider it. | |
| − | Proportion of the variance of TOP/BOTTOM tortuosity (variable Y) explained by global tortuosity (variable X independent) is between 60-70%. This means that the overall tortuosity of the veins/arteries explains a large proportion | ||
| − | |||
Since there is a difference between TOP and BOTTOM tortuosity we summarize this information in a new feature : asymmetry. How does tortuosity differ in the bottom and top of the retina vasculature? | Since there is a difference between TOP and BOTTOM tortuosity we summarize this information in a new feature : asymmetry. How does tortuosity differ in the bottom and top of the retina vasculature? | ||
| − | + | We plotted the distributions of the asymmetries for the veins/arteries. To see if it is significant, we compare this distribution to what the distribution looks like when the attribution top/bottom to the segments is random. | |
| − | We | + | We got a significant difference with the distribution of 10'000 retinas but not on 500. Although we find a very significant difference between the two distributions, the difference between the means of random and real asymmetry is very small. The random one is, as expected, centered around zero, while for both the veins and the arteries the distributions are shifted towards positive values (show on the formula), meaning more sinuous vessels at the top hemipsher |
So it's significant on 10'000 retinas but not on 500: Larger sample sizes provide more power to detect smaller effects, which is why we find a significant difference with 10,000 retinas but not with 500. | So it's significant on 10'000 retinas but not on 500: Larger sample sizes provide more power to detect smaller effects, which is why we find a significant difference with 10,000 retinas but not with 500. | ||
| − | Is this *practically significant* though? An effect can be statistically significant but may not be practically/biologically significant if the size of the effect is too small to matter in a practical sense. If the effect size is so small that it requires an enormous sample size to detect, one might question its practical significance or relevance. The difference are so small maybe the | + | Is this *practically significant* though? Is it biologically interesting? An effect can be statistically significant but may not be practically/biologically significant if the size of the effect is too small to matter in a practical sense. If the effect size is so small that it requires an enormous sample size to detect, one might question its practical significance or relevance. The difference are so small maybe the errors made by the software are sufficient to bias one observation and make its classification unreliable but this error cancels out on a very very large number of observations, which is what we have. |
| − | So there is an effect, but have to keep in mind it is very small. | + | So there is an effect, but have to keep in mind it is very small. |
| − | Now that we have this new value for asymmetry, which seems to encode the 'existing' difference that we have between the top tortuosity and the bottom tortuosity | + | Now that we have this new value for asymmetry, which seems to encode the 'existing' difference that we have between the top tortuosity and the bottom tortuosity, we need to know if this new information given by the asymmetry correlates with anything else to see if is really useful or simply redundant to other features already extracted from the images (IDP). The heatmap looked sound and asymmetry did not seem correlated with anything else, so appeared to be a useful new parameter. |
==Next steps of such an analysis== | ==Next steps of such an analysis== | ||
So the asymmetry is a new variable, and the first step would need to be to test the heritability, using a GWAS. GWAS stands for "Genome Wide Association Study" and is used to link a characteristic with a gene or a combination of genes. This was done and the preliminary results could indicate that this asymmetry trait does not have a huge genetic component. We would therefore need to test the environmental exposition aspect. The UK biobank dataset contains additional data such as sun exposure or diseases (skin cancer, cardiovascular), so the correlations have yet to be tested. Also we've been told that the TOP repeatedly has a bigger tortuosity, we could imagine the effects of the environment on that. | So the asymmetry is a new variable, and the first step would need to be to test the heritability, using a GWAS. GWAS stands for "Genome Wide Association Study" and is used to link a characteristic with a gene or a combination of genes. This was done and the preliminary results could indicate that this asymmetry trait does not have a huge genetic component. We would therefore need to test the environmental exposition aspect. The UK biobank dataset contains additional data such as sun exposure or diseases (skin cancer, cardiovascular), so the correlations have yet to be tested. Also we've been told that the TOP repeatedly has a bigger tortuosity, we could imagine the effects of the environment on that. | ||
| + | As the deep learning methods to perform segmentation of the fundus image are getting more and more reliable and precise, we can expect that a better segmentation of the images will allow the detection of more vessels, especially the small ones. And also decrease the errors in the labelling of veins and arteries. This more accurate segmentation and annotation will allow to compute more precise tortuosity values and so better asymmetry and analysis of the difference between top and bottom hemispheres. | ||
==Feedback== | ==Feedback== | ||
Revision as of 10:58, 31 May 2024
Jonathan NICOLET-DIT_FÉLIX, Bertille BOURG, Louis HEAU
Supervisor: Sacha BORS
To find out if there was a difference in tortuosity between top and bottom segments, we first put together a method to separate the blood vessels in two categories : TOP hemisphere and BOTTOM hemisphere, then we computed their tortuosity and concluded there was a very small positive asymmetry.
Contents
Presentation of the project: why is it important/relevant?
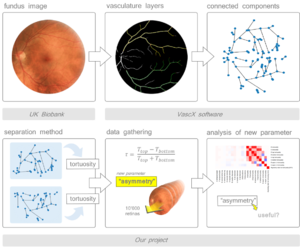
Retina fundus images are a type of picture taken by a special camera through the iris. They allow us to visualise the vasculature of the retina. This is a very convenient non-invasive way to obtain an insight of the body's vascular features, and the ultimate goal is to be able to use these pictures as a proxy for different diseases linked to vasculature such as ocular diseases (diabetic retinopathy, glaucoma) but also more general cardiovascular diseases like stroke, coronary heart disease or hypertension.
But to make the link between diseases and the retinal vasculature, we need to extract features (image derived phenotypes IDP) from the fundus images such as the number of bifurcation, the length of vessels, the evolution of the diameter, etc. One of the features that has recently drawn attention is tortuosity: how sinuous a blood vessel segment is compared to the direct length from its two extremities. Tortuosity is an important feature to study because it has potential links with cardiovascular diseases.
What is unknown is if there is a difference between the tortuosity in the top of the retina vs the bottom for arteries or veins.
Basic concepts
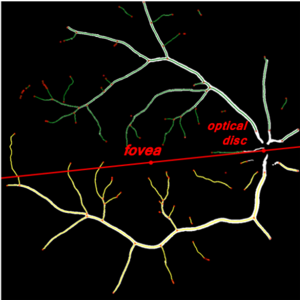
Indeed, when we look at a fundus image what is striking is that there are two large vascular networks above and below a line between the fovea and the optical disc. Arteries and veins are two stacked layers with different biological functions, so we compare them separately in the analysis. But we have these two sets. are they different ? especially for tortuosity ? Should we compute them separately in the analysis or can we use a "global tortuosity ? "
The dataset we will be using for the analysis is the UK biobank dataset, which contains for one patient their genome sequence, and a huge lot of various traits, including the fundus images from their retinas. With this dataset we have a great number of images. These images can be automatically analysed with a special python package based on machine learning methods that's being developed called vascX, that can extract features from the fundus images. The extracted features are stored in a retina object, containing many things such as a representation of the retina as a graph with edges and nodes, and the position of important features such as the optical disc (root of all the vasculature supplying the retinal cells ) and the fovea (focal point of an image on the retina, composed of the majority of the cones).
Our research goals
We want to compare the tortuosity value for each vessel layer (veins & arteries) for the top hemisphere and the bottom hemisphere of the retina. To do this, we first need a separation method in python for the top and bottom components. Once we have separated these, we need to compute the tortuosity for each hemisphere, and compare it to the global tortuosity. We want to see if there is a difference, an asymmetry, between top and bottom tortuosity. We will calculate an asymmetry coefficient and see if it correlates with any other retinal vasculature trait. Indeed, if it correlates with another feature that we already have, there is no need to calculate it since the information it would bring is already provided by this other feature.
Methods
Before computing the tortuosity, we need a method to separate the vascular elements between the top and the bottom. For this, we will use the graph representation in the 'retina' vascX output, retina.arteries.graph [.nodes/.edgdes, etc https://networkx.org/ ] or retina.veins.graph. This allows us to use the graph functions implemented in networkX.
We have thought about three methods to separate the connected components, the first one would be to take half the picture and everything that falhs above is "up" and everything below is "down". But this is not really precise as the images can be skewed.
A more precise way separation would be to use anchor points within the retina graph, such as the position of the fovea and the optical disc. we could then draw a line and consider again, everything above belonging to the top etc. But we still have a problem, because vessels are intertwined meaning that some bits from one side will cross over the line and we wrongly attributed.
To account to this, we took the connected components of the graphs, and calculated their barycentres. Their barycentres are the centers of the clusters. So it's a majority vote, and instead of deciding if the points are above or below the line, we decide if the cluster centres are above or below the line, then we attribute the rest of the cluster points to the orientation of the cluster center, and it is more likely to be accurate. This is the method we used for the final calculation.
Once we have this list of segments belonging to the top or the bottom for both the arteries and the veins, we can compute the tortuosity of each segment, and extract values such as the median tortuosity for the top/bottom and for the veins/arteries. We will also calculate the asymmetry coefficient with the following formula: Tau = \frac{tort_top - tort_bottom}{tort_top + tort_bottom}. The absolute value can be sometimes computed but then the orientation of a potential asymmetry is lost because without it we know that if the asymmetry is positive, the tortuosity of the top hemisphere is higher than the one at the bottom. We added a control to see if there is a real difference between top and bottom: we randomly attributed 'top' or 'bottom' to all of the vessels segments and calculated then the top and bottom tortuosity of those random hemisphere to compare it with the distribution of the asymmetry when top and bottom is attributed according to the real position of the vessel in the retina. After producing a dataframe of the new values, we switched to R for the statistical analysis.
Results
One other way of looking if the tortuosities are similar on the top/bottom to the global one, we can make linear regression models between the global tortuosity for arteries/veins and each regional tortuosity (top/bottom). We obtained coefficients of determination in the 0.6~0.75 range, suggesting a correlation, but not of 1, meaning that there is information in this half retina that is specific to it and that the global tortuosity cannot fully explain. One alternative hypothesis could be that when we plot the top tortuosity against the global tortuosity we lack half of the information to make the comparison which is the other half of the retina therefore we cannot explain the variance fully but if the tortuosity were equivalent between the top and the bottom, this "representative half" would be a much better estimator. We could still randomise the segments for the top/bottom tortuosities and see if we find the same values. If we do, then the low R² is because we lack values and if we don't it's because the information in the top/bottom section is specific to it. So when randomized, the R² become considerably higher compared to the non-randomized in the 500 retina sample. This means that still with half the data, we are able to explain the global tortuosity much better. The fact that it does not go higher is probably because the sample is not large enough (we did it on the 500 retinas and not the 10'000). Proportion of the variance of TOP/BOTTOM tortuosity (variable Y) explained by global tortuosity (variable X independent) is between 60-70%. This means that the overall tortuosity of the veins/arteries explains a large proportion of the variance observed in the tortuosity of the veins/arteries in the top or bottom hemisphere, although it is not a complete explanation. So this measure is not 100% redundant and we can consider it.
Since there is a difference between TOP and BOTTOM tortuosity we summarize this information in a new feature : asymmetry. How does tortuosity differ in the bottom and top of the retina vasculature? We plotted the distributions of the asymmetries for the veins/arteries. To see if it is significant, we compare this distribution to what the distribution looks like when the attribution top/bottom to the segments is random. We got a significant difference with the distribution of 10'000 retinas but not on 500. Although we find a very significant difference between the two distributions, the difference between the means of random and real asymmetry is very small. The random one is, as expected, centered around zero, while for both the veins and the arteries the distributions are shifted towards positive values (show on the formula), meaning more sinuous vessels at the top hemipsher
So it's significant on 10'000 retinas but not on 500: Larger sample sizes provide more power to detect smaller effects, which is why we find a significant difference with 10,000 retinas but not with 500. Is this *practically significant* though? Is it biologically interesting? An effect can be statistically significant but may not be practically/biologically significant if the size of the effect is too small to matter in a practical sense. If the effect size is so small that it requires an enormous sample size to detect, one might question its practical significance or relevance. The difference are so small maybe the errors made by the software are sufficient to bias one observation and make its classification unreliable but this error cancels out on a very very large number of observations, which is what we have. So there is an effect, but have to keep in mind it is very small.
Now that we have this new value for asymmetry, which seems to encode the 'existing' difference that we have between the top tortuosity and the bottom tortuosity, we need to know if this new information given by the asymmetry correlates with anything else to see if is really useful or simply redundant to other features already extracted from the images (IDP). The heatmap looked sound and asymmetry did not seem correlated with anything else, so appeared to be a useful new parameter.
Next steps of such an analysis
So the asymmetry is a new variable, and the first step would need to be to test the heritability, using a GWAS. GWAS stands for "Genome Wide Association Study" and is used to link a characteristic with a gene or a combination of genes. This was done and the preliminary results could indicate that this asymmetry trait does not have a huge genetic component. We would therefore need to test the environmental exposition aspect. The UK biobank dataset contains additional data such as sun exposure or diseases (skin cancer, cardiovascular), so the correlations have yet to be tested. Also we've been told that the TOP repeatedly has a bigger tortuosity, we could imagine the effects of the environment on that.
As the deep learning methods to perform segmentation of the fundus image are getting more and more reliable and precise, we can expect that a better segmentation of the images will allow the detection of more vessels, especially the small ones. And also decrease the errors in the labelling of veins and arteries. This more accurate segmentation and annotation will allow to compute more precise tortuosity values and so better asymmetry and analysis of the difference between top and bottom hemispheres.
Feedback
This project was really interesting. It allowed us to work on something concrete, which contrasted with the other courses, which were much more theoretical. It also enabled us to develop new skills and understand what real bioinformatics research is all about. The only problem we have identified is that the level required to complete this project is much higher than the level acquired during the bachelor's degree. It might be interesting to have one or two courses on the functionalities used.