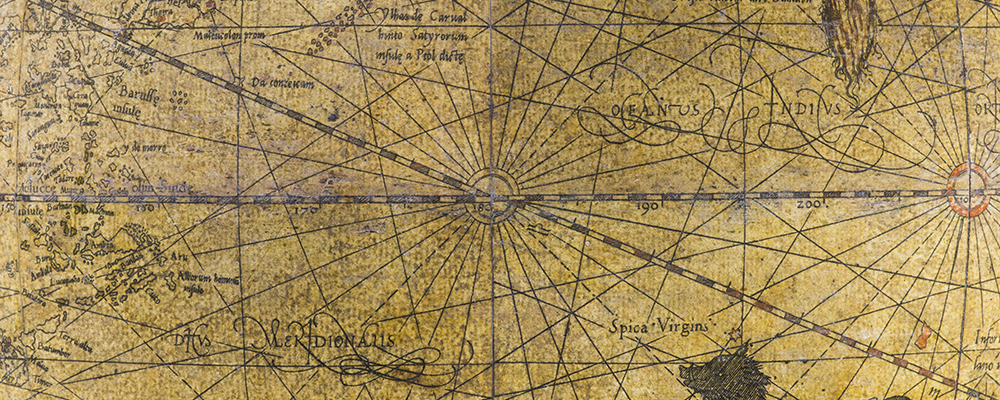
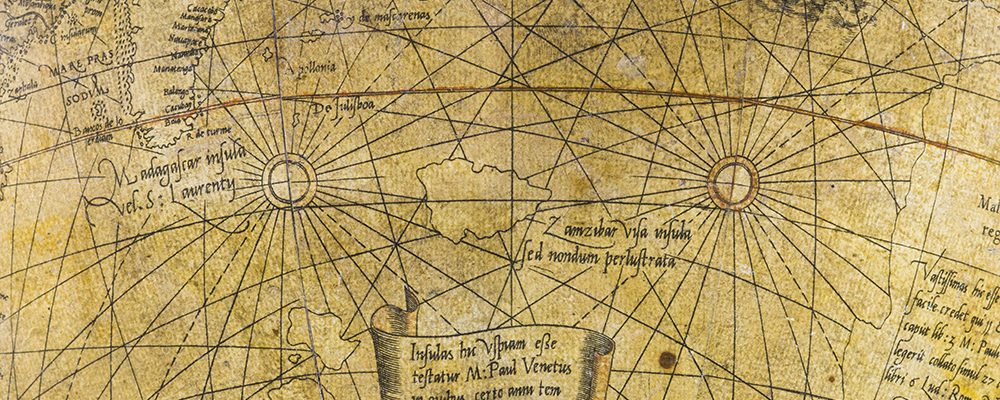
For the first time on a printed globe, Gerardus Mercator used a system of wind roses as starting points for rhumb lines.

From each wind rose 32 such lines fan out in all directions, showing the routes that ships could theoretically take on the high seas using the compass. Each rhumb line on Mercator’s terrestrial globe joins two points by crossing the intervening meridians at the same angle, creating the curve that a ship would have followed sailing on an unchanging course.

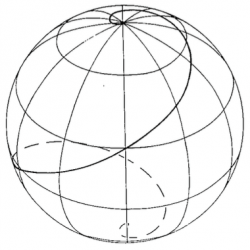
Drawing rhumb lines on a spherical surface is no simple matter. Although Mercator inherited the knowledge and skills needed to do so from his mentor, Gemma Frisius, he succeeded in transposing on the 3-dimensinal surface of his terrestrial globe the network of straight lines which had, until then, been incorrectly represented. He drew them on the gores in such a way that they became rhumb lines when laid on the sphere. He managed to do this superbly four years after the Portuguese geometer Pedro Nunez had imperfectly formulated the convergence of the meridians on a spherical surface, around 1537.

Perhaps wanting the terrestrial globe to be used as an onboard navigational instrument, Mercator came up with a crucial innovation for mariners even though the idea of using a globe on a ship was not really plausible for practical reasons that one can easily imagine. In 1569 he proposed a revolutionary solution that could at last be used: a planisphere, i.e. a projection of his terrestrial globe on a two-dimensional surface. This stroke of genius brought together portolan maps, based on the courses and durations of known sea voyages, and the maps of the Greeks, based on latitude and longitude.

In this case rhumb lines became straight trajectories on a Mercator projection. Mercator left no explanation of the procedure he used to achieve this conversion and it would not be until 1695 that the rhumb line equation was really worked out.